十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F )、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题: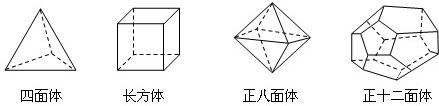
(1)根据上面多面体模型,完成表格中的空格:
| 多面体 |
顶点数(V) |
面数(F) |
棱数(E) |
| 四面体 |
4 |
4 |
6 |
| 长方体 |
8 |
6 |
12 |
| 正八面体 |
6 |
8 |
12 |
| 正十二面体 |
|
|
|
(2)你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是
(3)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是
(4)某个玻璃鉓品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为x个,八边形的个数为y个,x+y=
如图, ⊙O的半径为4㎝, 是⊙O的直径,
是⊙O的直径, 切⊙O于点
切⊙O于点 ,且
,且 =4㎝,当点P在⊙O上运动时,是否存在点P,使得△
=4㎝,当点P在⊙O上运动时,是否存在点P,使得△ 为等腰三角形,若存在,有几个符合条件的点
为等腰三角形,若存在,有几个符合条件的点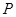 ,并分别求出点
,并分别求出点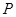 到线段
到线段 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由.
一张长方形桌子有6个座位.按甲方式将桌子拼在一起.

3张桌子拼在一起共有个座位,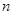 张桌子拼在一起共有个座位;
张桌子拼在一起共有个座位;按乙方式将桌子拼在一起.

3张桌子拼在一起共有个座位, 张桌子拼在一起共有个座位;
张桌子拼在一起共有个座位;某食堂有A,B两个餐厅,现有200张这样的长方形桌子,计划把这些桌子全放在两个餐厅,每个餐厅都要放有桌子.将
 张桌子放在A餐厅,按甲方式每6张拼成1张大桌子;将其余桌子都放在B餐厅,按乙方式每4张桌子拼成1张大桌子,若两个餐厅一共有790个座位,问A,B两个餐厅各有多少个座位?
张桌子放在A餐厅,按甲方式每6张拼成1张大桌子;将其余桌子都放在B餐厅,按乙方式每4张桌子拼成1张大桌子,若两个餐厅一共有790个座位,问A,B两个餐厅各有多少个座位?
为了调查某校全体初中生的视力变化情况,统计了每位初中生连续三年视力检查的结果(如图1),并统计了2010年全校初中生的视力分布情况(如图2、3).
|
|
从图1提供的信息用统计知识,预测2012年全校学生的视力在4.9及以下的学生人数(从一个角度预测即可);

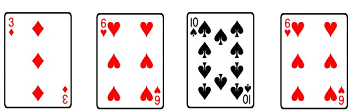
把4张普通扑克牌;方块3,红心6,黑桃10,红心6,洗匀后正面朝下放在桌面上.从中随机抽取一张牌是黑桃的概率是多少?
从中随机抽取一张,再从剩下的牌中随机抽取另一张. 请用表格或树状图表示抽取的两张牌牌面数字所有可能出现的结果,并求抽出一对6的概率.
在平面直角坐标中,直角三角板
 ,将直角顶点
,将直角顶点 放在点(
放在点( ,1)处,
,1)处, ∥
∥ ,求经过点C的反比例函数的解析式.
,求经过点C的反比例函数的解析式.