如图, ⊙O的半径为4㎝,
是⊙O的直径,
切⊙O于点
,且=4㎝,当点P在⊙O上运动时,是否存在点P,使得△
为等腰三角形,若存在,有几个符合条件的点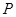
,并分别求出点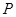到线段的距离；若不存在,请说明理由.
如图，已知矩形ABCD，AB=
，BC=3，在BC上取两点E，F（E在F左边），以EF为边作等边三角形PEF，使顶点P在AD上，PE，PF分别交AC于点G，H．
（1）求△PEF的边长；
（2）若△PEF的边EF在射线BC上移动（点E的移动范围在B、C之间，不与B、C两点重合）．设BE=x，PH=y．
①求y与x的函数关系式；
②连接BG，设△BEG面积为S，求S与x的函数关系式，判断x为何值时S最大，并求最大值S．
如图，一条直线与反比例函数
的图象交于A（1，4），B（4，n）两点，与x轴交于点D，AC⊥x轴，垂足为C．
（1）求反比例函数的解析式及D点的坐标；
（2）点P是线段AD的中点，点E，F分别从C，D两点同时出发，以每秒1个单位的速度沿CA，DC运动，到点A，C时停止运动，设运动的时间为t（s）．
①求证：PE=PF．
②若△PEF的面积为S，求S的最小值．
一个不透明的布袋里装有3个球，其中2个红球，1个白球，它们除颜色外其余都相同．
（1）求摸出1个球是白球的概率；
（2）摸出1个球，记下颜色后放回，并搅均，再摸出1个球．求两次摸出的球恰好颜色不同的概率（要求画树状图或列表）；
（3）现再将n个白球放入布袋，搅均后，使摸出1个球是白球的概率为
．求n的值．
如图，在一块长为22米，宽为17米的矩形地面上，要修建同样宽的两条互相垂直的道路（两条道路各与矩形的一条边平行），剩余部分种上草坪，使草坪面积为300平方米，那么道路的宽度应该是多少？
（1）如图1，正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上，连接BF、DF．求证：BF=DF；
（2）如图2，在△ABC中，∠B=46°，∠C=54°，AD平分∠BAC，交BC于D，DE∥AB，交AC于E，求∠ADE的度数．