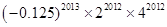如图，一条直线与反比例函数
的图象交于A（1，4），B（4，n）两点，与x轴交于点D，AC⊥x轴，垂足为C．
（1）求反比例函数的解析式及D点的坐标；
（2）点P是线段AD的中点，点E，F分别从C，D两点同时出发，以每秒1个单位的速度沿CA，DC运动，到点A，C时停止运动，设运动的时间为t（s）．
①求证：PE=PF．
②若△PEF的面积为S，求S的最小值．
如图是教师每天在黑板上书写用的粉笔，请画出图示粉笔俯视图.
用小立方体重新搭一几何体，使得它的俯视图和左视图与你在上图方格中所画的图一致，则搭建这样的新几何体最少要_______个小立方块，最多要_______个小立方块.
由大小相同的小立方块搭成的几何体如图，请在下图的方格中画出该几何体的俯视图和左视图.
回答下列问题：
⑴如图所示的甲、乙两个平面图形能折什么几何体？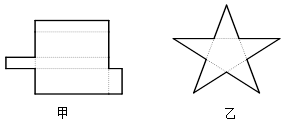
（2）由多个平面围成的几何体叫做多面体.若一个多面体的面数为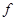
，顶点个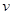数为
，棱数为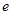
，分别计算第（1）题中两个多面体的
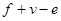的值？你发现什么规律？
（3）应用上述规律解决问题：一个多面体的顶点数比面数大8，且有50条棱，求这个几何体的面数.
阅读计算：
阅读下列各式：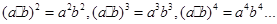
回答下列三个问题:
①验证: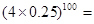 
__ .
__.
②通过上述验证， 归纳得出：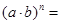
__；
__ .
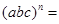请应用上述性质计算：