有甲、乙两个不透明的口袋,甲袋中有3个球,分别标有数字0,2,5;乙袋中有3个球,分别标有数字0,1,4.这6个球除所标数字以外没有任何其他区别.从甲、乙两袋中各随机摸出1个球,用画树状图(或列表)的方法,求摸出的两个球上数字只和是6的概率.
先化简,再求值::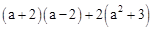 ,其中a=
,其中a= .
.
如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.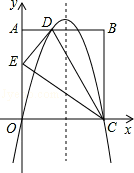
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P、Q、C为顶点的三角形与△ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
(1)求证:直线PA为⊙O的切线;
(2)试探究线段EF、OD、OP之间的等量关系,并加以证明;
(3)若BC=6,tan∠F= ,求cos∠ACB的值和线段PE的长.
,求cos∠ACB的值和线段PE的长.
根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2012年5月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见下表:
| 一户居民一个月用电量的范围 |
电费价格(单位:元/千瓦时) |
| 不超过150千瓦时 |
a |
| 超过150千瓦时但不超过300千瓦时的部分 |
b |
| 超过300千瓦时的部分 |
a+0.3 |
2012年5月份,该市居民甲用电100千瓦时,交电费60元;居民乙用电200千瓦时,交电费122.5元.该市一户居民在2012年5月以后,某月用电x千瓦时,当月交电费y元.
(1)上表中,a= ;b= ;
(2)请直接写出y与x之间的函数关系式;
(3)试行“阶梯电价”收费以后,该市一户居民月用电多少千瓦时时,其当月的平均电价每千瓦时不超过0.62元?