如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.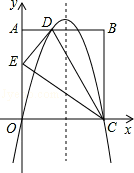
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P、Q、C为顶点的三角形与△ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
【操作发现】
(1)如图1, 为等边三角形,先将三角板中的 角与 重合,再将三角板绕点 按顺时针方向旋转(旋转角大于 且小于 ,旋转后三角板的一直角边与 交于点 ,在三角板斜边上取一点 ,使 ,线段 上取点 ,使 ,连接 , .
①求 的度数;
② 与 相等吗?请说明理由;
【类比探究】
(2)如图2, 为等腰直角三角形, ,先将三角板的 角与 重合,再将三角板绕点 按顺时针方向旋转(旋转角大于 且小于 ,旋转后三角板的一直角边与 交于点 ,在三角板另一直角边上取一点 ,使 ,线段 上取点 ,使 ,连接 , .请直接写出探究结果:
① 的度数;
②线段 , , 之间的数量关系.

数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:当温度达到设定温度 时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到 时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至 时,制冷再次停止, ,按照以上方式循环进行.
同学们记录了 内15个时间点冷柜中的温度 随时间 的变化情况,制成下表:
|
时间 |
|
4 |
8 |
10 |
16 |
20 |
21 |
22 |
23 |
24 |
28 |
30 |
36 |
40 |
42 |
44 |
|
|
温度 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)通过分析发现,冷柜中的温度 是时间 的函数.
①当 时,写出一个符合表中数据的函数解析式 ;
②当 时,写出一个符合表中数据的函数解析式 ;
(2) 的值为 ;
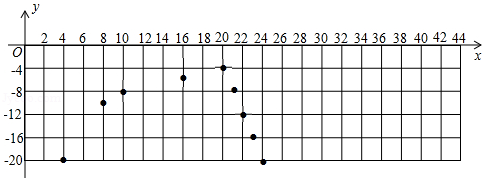
(3)如图,在直角坐标系中,已描出了上表中部分数据对应的点,请描出剩余数据对应的点,并画出当 时温度 随时间 变化的函数图象.
今年,我市某中学响应习总书记“足球进校园”的号召,开设了“足球大课间”活动,现需要购进100个某品牌的足球供学生使用.经调查,该品牌足球2015年单价为200元,2017年单价为162元.
(1)求2015年到2017年该品牌足球单价平均每年降低的百分率;
(2)选购期间发现该品牌足球在两个文体用品商场有不同的促销方案:

试问去哪个商场购买足球更优惠?
主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
.放下自我,彼此尊重;
.放下利益,彼此平衡;
.放下性格,彼此成就;
.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟,根据同学们的选择情况,小明绘制了如图两幅不完整的图表,请根据图表中提供的信息,解答下列问题:
|
观点 |
频数 |
频率 |
|
|
|
0.2 |
|
|
12 |
0.24 |
|
|
8 |
|
|
|
20 |
0.4 |
(1)参加本次讨论的学生共有 人;
(2)表中 , ;
(3)将条形统计图补充完整;
(4)现准备从 , , , 四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点 (合理竞争,合作双赢)的概率.

如图1,抛物线 经过平行四边形 的顶点 、 、 ,抛物线与 轴的另一交点为 .经过点 的直线 将平行四边形 分割为面积相等的两部分,与抛物线交于另一点 .点 为直线 上方抛物线上一动点,设点 的横坐标为 .
(1)求抛物线的解析式;
(2)当 何值时, 的面积最大?并求最大值的立方根;
(3)是否存在点 使 为直角三角形?若存在,求出 的值;若不存在,说明理由.
