【操作发现】
(1)如图1, 为等边三角形,先将三角板中的 角与 重合,再将三角板绕点 按顺时针方向旋转(旋转角大于 且小于 ,旋转后三角板的一直角边与 交于点 ,在三角板斜边上取一点 ,使 ,线段 上取点 ,使 ,连接 , .
①求 的度数;
② 与 相等吗?请说明理由;
【类比探究】
(2)如图2, 为等腰直角三角形, ,先将三角板的 角与 重合,再将三角板绕点 按顺时针方向旋转(旋转角大于 且小于 ,旋转后三角板的一直角边与 交于点 ,在三角板另一直角边上取一点 ,使 ,线段 上取点 ,使 ,连接 , .请直接写出探究结果:
① 的度数;
②线段 , , 之间的数量关系.

如图,△ABC内接于⊙O,BC是⊙O的直径,OE⊥AC,垂足为E,过点A作⊙O的切线与BC的延长线交于点D,sinD=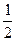 ,OD=20.
,OD=20.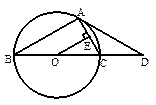
( 1)求∠ABC的度数;
1)求∠ABC的度数;
(2)连接BE,求线段BE的长.
列方程或方程组解应用题:
如 图,要建一个面积为40平方米的矩形花园ABCD,为了节约材料,花园的一边AD靠着原有的一面墙,墙长为8米(AD<8),另三边用栅栏围成,已知栅栏总长为24米,求花园一边AB的长.
图,要建一个面积为40平方米的矩形花园ABCD,为了节约材料,花园的一边AD靠着原有的一面墙,墙长为8米(AD<8),另三边用栅栏围成,已知栅栏总长为24米,求花园一边AB的长.
已知:如图,正方形ABCD的边长为6,将其绕点A顺时针旋转30°得到正方形AEFG,FG与B C相交于点H.
C相交于点H.
(1)求证:BH=GH;
(2)求BH的长.
如图,直线 与x轴交于点A,与y轴交于点B.
与x轴交于点A,与y轴交于点B.
(1)求点A、B的坐标
(2)若点P在直线 上,且横坐标为-2,
上,且横坐标为-2,
求过点P的反比例函数图象的解析式.
解分式方程 .
.