如图1,抛物线 经过平行四边形 的顶点 、 、 ,抛物线与 轴的另一交点为 .经过点 的直线 将平行四边形 分割为面积相等的两部分,与抛物线交于另一点 .点 为直线 上方抛物线上一动点,设点 的横坐标为 .
(1)求抛物线的解析式;
(2)当 何值时, 的面积最大?并求最大值的立方根;
(3)是否存在点 使 为直角三角形?若存在,求出 的值;若不存在,说明理由.

如图,在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长,与BC的延长线交于点F.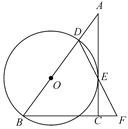
(1)求证:DE=FE;
(2)若BC=9,AD=6,求BF的长.
认真观察图1的4个图中阴影部分构成的图案,回答下列问题:

(1)请写出这四个图案都具有的两个共同特征.
特征1:;特征2:.
(2)请在图2中设计出你心中的图案,使它也具备你所写出的上述两个特征.
2013年3月1日,张老师就本班学生对心理健康知识的了解程度进行了一次调查统计,下图是他采集数据后绘制的两幅不完整的统计图(A:不了解,B:一般了解,C:了解较多,D:熟悉).请你根据图中提供的信息解答以下问题:

(1)求该班共有多少名学生;
(2)在条形统计图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数.
某地区冬季干旱,康平社区每天需从外地调运饮用水60吨.有关部门紧急部署,从甲、乙两水厂调运饮用水到供水点,甲厂每天最多可调出40吨,乙厂每天最多可调出45吨.从两水厂运水到康平社区供水点的路程和运费如下表:
| 到康平社区供水点的路程(千米) |
运费(元/吨·千米) |
|
| 甲厂 |
20 |
4 |
| 乙厂 |
14 |
5 |
(1)若某天调运水的总运费为4450元,则从甲、乙两水厂各调运了多少吨饮用水?
(2)设从甲厂调运饮用水x吨,总运费为W元,试写出W关于x的函数关系式,并确定x的取值范围.怎样安排调运方案才能使每天的总运费最省?
如图,在□ABCD中,AB=4,AD=6,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=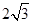 .
.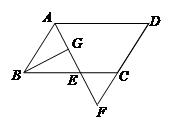
(1)求AE的长;(2)求ΔCEF的周长和面积.