某地区冬季干旱,康平社区每天需从外地调运饮用水60吨.有关部门紧急部署,从甲、乙两水厂调运饮用水到供水点,甲厂每天最多可调出40吨,乙厂每天最多可调出45吨.从两水厂运水到康平社区供水点的路程和运费如下表:
| |
到康平社区供水点的路程(千米) |
运费(元/吨·千米) |
| 甲厂 |
20 |
4 |
| 乙厂 |
14 |
5 |
(1)若某天调运水的总运费为4450元,则从甲、乙两水厂各调运了多少吨饮用水?
(2)设从甲厂调运饮用水x吨,总运费为W元,试写出W关于x的函数关系式,并确定x的取值范围.怎样安排调运方案才能使每天的总运费最省?
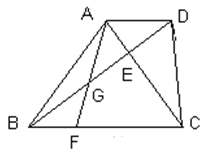
已知AD⊥BC,BE=CE,∠ABC=2∠C,BF为∠B的平分线.求证:AB=2DE.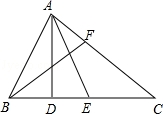
如图,在△ABC中,AB=AC,AD平分∠BAC.求证:∠DBC=∠DCB.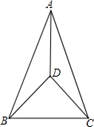
如图,已知在Rt△ABC中,∠ACB=90°,AB=10,tanA=4/3,点D是斜边AB上的动点,连接CD,作DE⊥CD,交射线CB于点E,设AD=x。(1)当点D是边AB的中点时,求线段DE的长;(2)当△BED是等腰三角形时,求x的值;(3)如果y=DE/DB。求y关于x的函数解析式,并写出它的定义域。
已知在平面直角坐标系xoy中,二次函数y=-2x²+bx+c的图像经过点A(-3,0)和点B(0,6)。(1)求此二次函数的解析式;(2)将这个二次函数的图像向右平移5个单位后的顶点设为C,直线BC与x轴相交于点D,求∠sin∠ABD;(3)在第(2)小题的条件下,连接OC,试探究直线AB与OC的位置关系,并且说明理由。
已知:r如图,在梯形ABCD中,AD∥BC,∠BCD=90°.对角线AC、BD相交于点E。且AC⊥BD。(1)求证:CD²=BC·AD;(2)点F是边BC上一点,连接AF,与BD相交于点G,如果∠BAF=∠DBF,求证: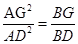 。
。