王师傅用4根木条钉成一个四边形木架(如图所示),要使这个木架不变形,他至少还要再钉上几根木条?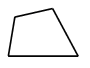
| A.0根 | B.1根 | C.2根 | D.3根 |
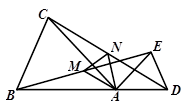
已知:如图所示,在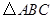 和
和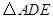 中,
中, ,
,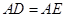 ,
,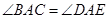 ,且点
,且点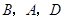 在同一条直线上,连接
在同一条直线上,连接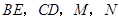 分别为
分别为 的中点, 连接
的中点, 连接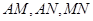 .
.
(1)求证: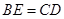 ; (4分)
; (4分)
(2)求证: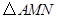 是等腰三角形.
是等腰三角形.
D是等边三角形内一点,DB=DA,BP=AB,∠DBP=∠DBC,求∠BPD的度数.
仔细阅读下面例题,解答问题:
例题:已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得
x2﹣4x+m=(x+3)(x+n)
则x2﹣4x+m=x2+(n+3)x+3n
∴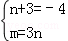
解得:n=﹣7,m=﹣21
∴另一个因式为(x﹣7),m的值为﹣21
问题:仿照以上方法解答下面问题:
已知二次三项式2x2+3x﹣k有一个因式是(2x﹣5),求另一个因式以及k的值.
作图题(不写作法)
已知:如下图所示.
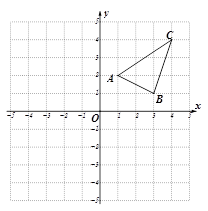
作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1三个顶点的坐标;
②.在x轴上确定点P,使PA+PC最小.