如图,在平面直角坐标系中,直线l是第一、三象限的角平分线
实验与探究: 
(1)由图观察易知A(0,2)关于直线l的对称点
 的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5) 关于直线l的对称点
的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5) 关于直线l的对称点 、
、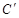 的位置,并写出他们的坐标:
的位置,并写出他们的坐标:  、
、 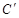 ;
;
归纳与发现:(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点
 的坐标为
的坐标为
运用与拓广:(3)已知两点D(1,-3)、E(-1,-4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
“校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的 看法,统计整理并制作了如下的统计图:
看法,统计整理并制作了如下的统计图: 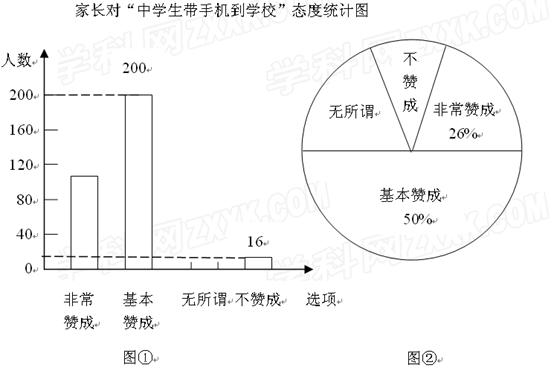
(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
(2)求图②中表示家长“无所谓”的圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少?
解不等式组 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.
(本小题满分9分,其中(1)小题4分,(2)小题5分)
某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)
| 甲 |
乙 |
|
| 进价(元/件) |
15 |
35 |
| 售价(元/件) |
20 |
45 |
(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?
(本小题满分9分,其中(1)小题5分,(2)小题4分)
如图4:在△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,点E是BC上一个动点(点E与B、C不重合),连接A、E.若a、b满足 ,且c是不等式组
,且c是不等式组 的最大整数解.
的最大整数解.
(1)求a、b、c的长.
(2)若AE平分△ABC的周长,求∠BEA的大小.
(本小题满分8分)列方程解应用题:
现加工一批机器零件,甲单独完成需4天,乙单独完成需6天。现由乙先做1天,然后两人合做,完成后共得报酬600元。若按个人完成的工作量给付报酬,你应如何分配呢?