如图,在平面直角坐标系中,顶点为(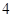 ,
,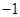 )的抛物线交
)的抛物线交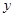 轴于
轴于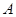 点,交
点,交 轴于
轴于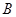 ,
,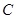 两点(点
两点(点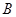 在点
在点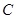 的左侧). 已知
的左侧). 已知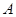 点坐标为(
点坐标为( ,
,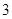 ).
). 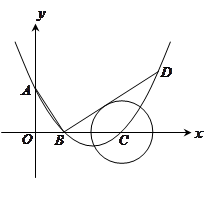
(1)求此抛物线的解析式;
(2)过点
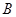 作线段
作线段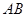 的垂线交抛物线于点
的垂线交抛物线于点 , 如果以点
, 如果以点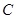 为圆心的圆与直线
为圆心的圆与直线 相切,请判断抛物线的对称轴
相切,请判断抛物线的对称轴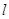 与⊙
与⊙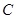 有怎样的位置关系,并给出证明;
有怎样的位置关系,并给出证明;(3)已知点
 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于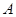 ,
,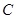 两点之间,问:当点
两点之间,问:当点 运动到什么位置时,
运动到什么位置时,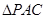 的面积最大?并求出此时
的面积最大?并求出此时 点的坐标和
点的坐标和 的最大面积.
的最大面积.
【问题提出】
学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.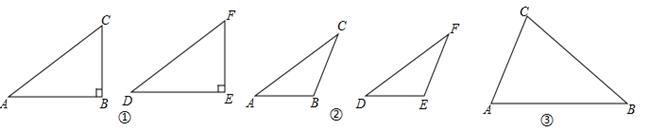
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,若,则△ABC≌△DEF.
如图,在Rt△ABC中,∠ACB=90°,AC="4" cm ,BC="3" cm,⊙O为△ABC的内切圆.
(1)求⊙O的半径;
(2)点P从点B沿边BA向点A以点1cm/s 的速度匀速运动,以点P为圆心,PB长为半径作圆.设点P运动的时间为 t s.若⊙P与⊙O相切,求t的值.
从甲地到乙地,先是一段平路,然后是一段上坡路。小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间。假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km。设小明出发xh后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.
(1)小明骑车在平路上的速度为km/h;他途中休息了h;
(2)求线段AB,BC所表示的y与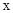 之间的函数关系式;
之间的函数关系式;
(3)如果小明两次经过途中某一地点的时间间隔为0.15h,那么该地点离甲地多远?
已知二次函数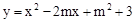 (m是常数)
(m是常数)
(1)求证:不论m为何值,该函数的图像与x轴没有公共点;
(2)把该函数的图像沿x轴向下平移多少个单位长度后,得到的函数的图像与x轴只有一个公共点?
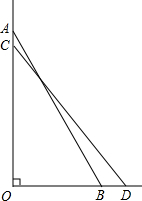
如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=51°18′,求梯子的长.
(参考数据:sin51°18′≈0.780,cos51°18′≈0.625,tan51°18′≈1.248)