(本小题满分12分)中心在原点,焦点在x轴上的椭圆C上的点到焦点距离的最大值为3,最小值为1.
(1)求椭圆C的方程;
(2)若直线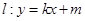 与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求该定点的坐标.
与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求该定点的坐标.
对于定义域为 的函数
的函数 ,若有常数M,使得对任意的
,若有常数M,使得对任意的 ,存在唯一的
,存在唯一的 满足等式
满足等式 ,则称M为函数
,则称M为函数 f (x)的“均值”.
f (x)的“均值”.
(1)判断1是否为函数 ≤
≤ ≤
≤ 的“均值”,请说明理由;
的“均值”,请说明理由;
(2)若函数
 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围;
(3)若函数 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数 的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
说明:对于(3),将根据结论的完整性与一般性程度给予不同的评分
已知数列 是各项均为正数的等差数列,公差为d(d
是各项均为正数的等差数列,公差为d(d  0).在
0).在 之间和b,c之间共插入
之间和b,c之间共插入 个实数,使得这
个实数,使得这 个数构成等比数列,其公比为q.
个数构成等比数列,其公比为q.
(1)求证: ;
;
(2)若 ,求
,求 的值;
的值;
(3)若插入的n个数中,有s个位于a,b之间,t个位于b,c之间,且 都为奇数,试比较s与t的大小,并求插入的n个数的乘积(用
都为奇数,试比较s与t的大小,并求插入的n个数的乘积(用 表示).
表示).
已知椭圆 :
: (
( )过点
)过点 ,其左、右焦点分别为
,其左、右焦点分别为 ,且
,且 .
.
(1)求椭圆 的方程;
的方程;
(2)若 是直线
是直线 上的两个动点,且
上的两个动点,且 ,则以
,则以 为直径的圆
为直径的圆 是否过定点?请说明理由.
是否过定点?请说明理由.
某校10名学生组成该校“科技创新周”志愿服务队(简称“科服队”),他们参加活动的有关数据统计如下:
| 参加活动次数 |
1 |
2 |
3 |
| 人 数 |
2 |
3 |
5 |
(1)从“科服队”中任选3人,求这3人参加活动次数各不相同的概率;
(2)从“科服队”中任选2人,用 表示这2人参加活动次数之差的绝对值,求随机变量
表示这2人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
已知矩形 内接于圆柱下底面的圆
内接于圆柱下底面的圆 ,
, 是圆柱的母线,若
是圆柱的母线,若 ,
, ,此圆柱的体积为
,此圆柱的体积为 ,求异面直线
,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
