(本小题满分12分)统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为:
 .已知甲、乙两地相距100千米.
.已知甲、乙两地相距100千米.
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
(本小题满分12分)有A、B、C、D、E五位工人参加技能竞赛培训.现分别从A、B二人在培训期间参加的若干次预赛成绩中随机抽取8次.用茎叶图表示这两组数据如下:
(Ⅰ) 现要从A、B中选派一人参加技能竞赛,从平均状况和方差的角度考虑,你认为派哪位工人参加合适?请说明理由;
(Ⅱ) 若从参加培训的5位工人中选2人参加技能竞赛,求A、B二人中至少有一人参加技能竞赛的概率.
(本小题满分12分)
已知等差数列 中,
中,
 为数列
为数列 的前
的前 项和.
项和.
(1)求数列 的通项公式;
的通项公式;
(2) 若数列 的公差为正数,数列
的公差为正数,数列 满足
满足 , 求数列
, 求数列 的前
的前 项和
项和
(本小题满分10分)选修4-5:不等式选讲
设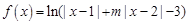 (
(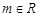 )
)
(Ⅰ)当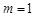 时,求函数
时,求函数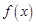 的定义域;
的定义域;
(Ⅱ)若当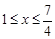 ,
,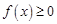 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分10分)选修4—4;坐标系与参数方程.
已知直线
 为参数), 曲线
为参数), 曲线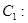
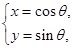 (
( 为参数).
为参数).
(Ⅰ)设 与
与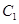 相交于
相交于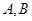 两点,求
两点,求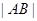 ;
;
(Ⅱ)若把曲线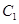 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的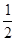 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的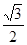 倍,得到曲线
倍,得到曲线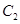 ,设点
,设点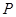 是曲线
是曲线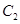 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值.
(本小题满分12分)已知函数
 .
.
(Ⅰ)当 时,讨论
时,讨论 的单调性;
的单调性;
(Ⅱ)当 时,对于任意的
时,对于任意的 ,证明:不等式
,证明:不等式