如果一个数列的各项都是实数,且从第二项起,每一项与它的前一项的平方差是同一个常数,则称该数列为等方差数列,这个常数叫这个数列的公方差.
(Ⅰ)若数列 既是等方差数列,又是等差数列,求证:该数列是常数列;
既是等方差数列,又是等差数列,求证:该数列是常数列;
(Ⅱ)已知数列 是首项为
是首项为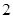 ,公方差为
,公方差为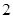 的等方差数列,数列
的等方差数列,数列 的前
的前 项和为
项和为 ,且满足
,且满足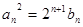 .若不等式
.若不等式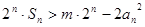 对
对 恒成立,求
恒成立,求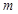 的取值范围.
的取值范围.
(本小题满分14分)数列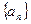 中,
中,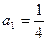 ;
; ,对任意的
,对任意的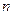 为正整数都有
为正整数都有 。
。
(1)求证: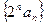 是等差数列;
是等差数列;
(2)求出
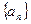 的通项公式
的通项公式 ;
;
(3)若 (
(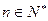 ),是否存在实数
),是否存在实数 使得
使得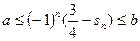 对任意的
对任意的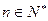 恒成立?若存在,找出
恒成立?若存在,找出 ;若不存在,请说明理由。
;若不存在,请说明理由。
已知圆C:
(1)若平面上有两点A(1 , 0),B(-1 , 0),点P是圆C上的动点,求使 取得最小值时点P的坐标.
取得最小值时点P的坐标.
(2) 若 是
是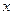 轴上的动点,
轴上的动点,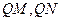 分别切圆
分别切圆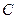 于
于 两点
两点
①若 ,求直线
,求直线 的方程;
的方程;
②求证:直线 恒过一定点.
恒过一定点.
(本小题满分12分)已知函数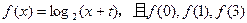 成等差数列,点
成等差数列,点 是函数
是函数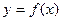 图像上任意一点,点
图像上任意一点,点 关于原点的对称点
关于原点的对称点 的轨迹是函数
的轨迹是函数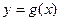 的图像。
的图像。
(1)解关于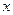 的不等式
的不等式 ;
;
(2)当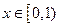 时,总有
时,总有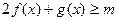 恒成立,求
恒成立,求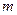 的取值范围.
的取值范围.
(本小题满分12分).如图所示,四棱锥P-ABCD,底面ABCD是边长为2的正方形,PA⊥面ABCD,PA=2,过点A作AE⊥PB,AF⊥PC,连接EF.
(1)求证:PC⊥面AEF.
(2)若面AEF交侧棱PD于点G( 图中未标出点G),求多面体P—AEFG的体积。
图中未标出点G),求多面体P—AEFG的体积。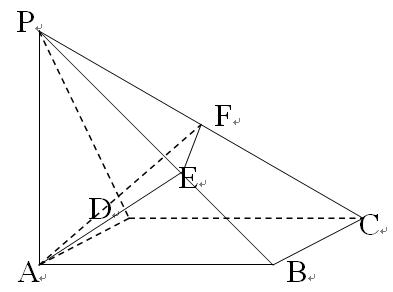
(本小题满分12分)在△ABC中,已知内角A、B、C所对的边分别为a、b、c,
且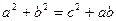
(1) 若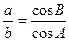 ,且
,且 ,求
,求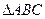 的面积;
的面积;
(2)已知向量 ,
, ,求|
,求| |的取值范围.
|的取值范围.