(本小题满分14分)已知函数 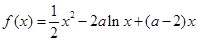 ,
, .
.
(Ⅰ)当 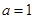 时,求函数
时,求函数 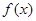 的最小值;
的最小值;
(Ⅱ)当 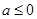 时,讨论函数
时,讨论函数 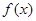 的单调性;
的单调性;
(Ⅲ)是否存在实数 ,对任意的
,对任意的  ,且
,且 ,有
,有 ,恒成立,若存在求出
,恒成立,若存在求出 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
(本小题满分15分)
若函数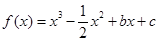 在
在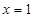 时取得极值,且当
时取得极值,且当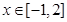 时,
时, 恒成立.
恒成立.
(1)求实数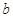 的值;
的值;
(2)求实数 的取值范围.
的取值范围.
(本小题满分14分)
已知椭圆
 ,其左准线为
,其左准线为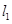 ,右准线为
,右准线为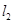 ,抛物线
,抛物线 以坐标原点
以坐标原点 为顶点,
为顶点,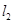 为准线,
为准线, 交
交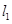 于
于 两点.
两点.
(1)求抛物线 的标准方程;
的标准方程;
(2)求线段 的长度.
的长度.
(本小题满分14分)
命题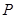 :函数
:函数 在
在 上是增函数;命题
上是增函数;命题 :
: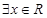 ,使得
,使得 .
.
(1)若命题“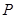 且
且 ”为真,求实数
”为真,求实数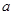 的取值范围;
的取值范围;
(2)若命题“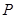 或
或 ”为真,“
”为真,“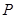 且
且 ”为假,求实数
”为假,求实数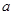 的取值范围.
的取值范围.
已知梯形ABCD中,AD∥BC,∠ABC ="∠BAD" =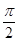 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,且EF∥BC。设AE =
,AB=BC=2AD=4,E、F分别是AB、CD上的点,且EF∥BC。设AE =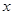 ,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
(1)当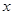 =2时,求证:BD⊥EG ;
=2时,求证:BD⊥EG ;
(2)若以F、B、C、D为顶点的三棱锥的体积记为 ,求
,求 的最大值;
的最大值;
(3)当 取得最大值时,求二面角D-BF-E的余弦值.
取得最大值时,求二面角D-BF-E的余弦值.
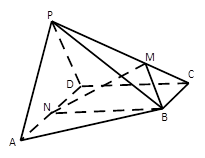
如图,四棱锥 的侧面
的侧面 垂直于底面
垂直于底面 ,
,
 ,
,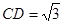 ,
, 在棱
在棱 上,
上,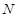 是
是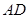 的中点,二面角
的中点,二面角 为
为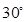 求
求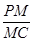 的值;
的值;