(本小题满分16分)如图,平面直角坐标系 中,
中, 和
和 为等腰直角三角形,
为等腰直角三角形, ,
, 设
设 和
和 的外接圆圆心分别为
的外接圆圆心分别为 .
.
(Ⅰ)若圆M与直线 相切,求直线
相切,求直线 的方程;
的方程;
(Ⅱ)若直线 截圆N所得弦长为4,求圆N的标准方程;
截圆N所得弦长为4,求圆N的标准方程;
(Ⅲ)是否存在这样的圆N,使得圆N上有且只有三个点到直线 的距离为
的距离为 ,若存在,求此时圆N的标准方程;若不存在,说明理由.
,若存在,求此时圆N的标准方程;若不存在,说明理由.
已知数列 是公差大于零的等差数列,数列
是公差大于零的等差数列,数列 为等比数列,且
为等比数列,且

(1)求数列 和
和 的通项公式
的通项公式
(2)设 ,求数列
,求数列 前n项和
前n项和 .
.
已知函数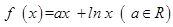 .
.
(1)若a=2,求曲线y=f(x)在x=1处的切线方程;
(2)求f(x)的单调区间;
(3)设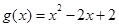 ,若对任意
,若对任意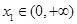 ,均存在
,均存在 ,使得
,使得 ,求a的取值范围.
,求a的取值范围.
已知椭圆E: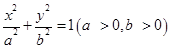 的离心率
的离心率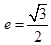 ,并且经过定点
,并且经过定点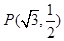
(1)求椭圆E 的方程;
(2)问是否存在直线y=-x+m,使直线与椭圆交于A, B 两点,满足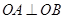 ,若存在求m 值,若不存在说明理由.
,若存在求m 值,若不存在说明理由.
一个多面体的直观图及三视图如图所示,其中M , N 分别是AF、BC 的中点,
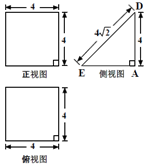
(1)求证:MN // 平面CDEF ;
(2)求二面角A-CF-B 的余弦值;
一企业某次招聘新员工分笔试和面试两部分,人力资源部经理把参加笔试的40名学生的成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100),得到频率分布直方图如图所示: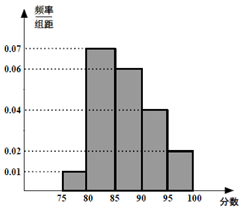
(1)分别求成绩在第4,5组的人数;
(2)若该经理决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6名进入面试,
①已知甲和乙的成绩均在第3组,求甲和乙同时进入面试的概率;
②若经理决定在这6名学生中随机抽取2名学生接受考官D的面试,设第4组中有X名学生被考官D面试,求X的分布列和数学期望.