以初速度v0竖直上抛一个质量为m的物体,设物体在运动过程中所受到的阻力的大小不变,物体经过时间t到达最高点O,
求:(1)物体由最高点落回原地所用的时间.
(2)物体落回原地时的速度大小
在电场中把电量为10-8C的负电荷从A点移到B点,电场力做功10-6J;再把它从B点移到C点,克服电场力做功3×10-6J。则A,B,C三点中哪点电势最高?A与C间电势差UAC为多少?
如图所示,竖直放置的圆弧轨道和水平轨道两部分相连. 水平轨道的右侧有一质量为 2 m的滑块C 与轻质弹簧的一端相连,弹簧的另一端固定在竖直的墙M上,弹簧处于原长时,滑块C静止在P 点处;在水平轨道上方O 处,用长为L 的细线悬挂一质量为 m 的小球 B,B 球恰好与水平轨道相切,并可绕O点在竖直平面内摆动。质量为 m 的滑块A 由圆弧轨道上静止释放,进入水平轨道与小球B发生碰撞,A、B 碰撞前后速度发生交换. P 点左方的轨道光滑、右方粗糙,滑块A、C 与PM 段的动摩擦因数均为
B,B 球恰好与水平轨道相切,并可绕O点在竖直平面内摆动。质量为 m 的滑块A 由圆弧轨道上静止释放,进入水平轨道与小球B发生碰撞,A、B 碰撞前后速度发生交换. P 点左方的轨道光滑、右方粗糙,滑块A、C 与PM 段的动摩擦因数均为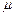 =0.5,A、B、C 均可视为质点
=0.5,A、B、C 均可视为质点 ,重力加速度为g.
,重力加速度为g.
(1)求滑块A 从2L高度处由静止开始下滑, 与B碰后瞬间B的速度.
(2)若滑块A 能以与球B 碰前瞬间相同的速度与滑块C 相碰,A 至少要从距水平轨道多高的地方开始释放?
(3)在(2)中算出的最小值高度处由静止释放A,经一段时间A 与C 相碰,设碰撞时间极短, 碰后一起压缩弹簧,弹簧最大压缩量为
碰后一起压缩弹簧,弹簧最大压缩量为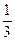 L,求弹簧的最大弹性势能。
L,求弹簧的最大弹性势能。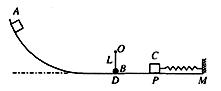
如图所示,在倾角为θ=37°的足够长的斜面上,有质量为m1=2kg的长木板。开始时,长木板上有一质量为m2=1kg的小铁块(视为质点)以相对地面的初速度
v0=2m/s 从长木板的中点沿长木板向下滑动,同时长木板在沿斜面向上的拉力作用下始终做速度为v=1m/s的匀速运动,小铁块最终与长木板一起沿斜面向上做匀速运动。已知小铁块与长木板、长木板与斜面间的动摩擦因数均为μ=0.9,重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8
试求:(1)小铁块在长木板上滑动时的加速度;
(2)长木板至少多长?
(3)在小铁块从木板中点运动到与木板速度相同的过程中拉力做了多少功?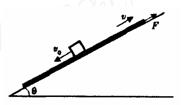
“嫦娥一号”探月卫星的成功发射,实现了中华民族千年奔月的梦想 。假若我国的航天员登上某一星球并在该星球表面上做了如下图所示的力学实验:让质量为m=1.0kg的小滑块以v0=1m/s的初速度从倾角为53°的斜面AB的顶点A滑下,到达B点后恰好能沿倾角为37°的斜面到达C点。不计滑过B点时的机械能损失,滑块与斜面间的动摩擦因数均为
。假若我国的航天员登上某一星球并在该星球表面上做了如下图所示的力学实验:让质量为m=1.0kg的小滑块以v0=1m/s的初速度从倾角为53°的斜面AB的顶点A滑下,到达B点后恰好能沿倾角为37°的斜面到达C点。不计滑过B点时的机械能损失,滑块与斜面间的动摩擦因数均为 ,测得A、C两点离B点所在水平面的高度分别为h1=1.2m,h2=0.5m。已知sin37°=0.6,cos37°=0.8,不计该星球的自转以及其他星球对它的作用。
,测得A、C两点离B点所在水平面的高度分别为h1=1.2m,h2=0.5m。已知sin37°=0.6,cos37°=0.8,不计该星球的自转以及其他星球对它的作用。
(1)求该星球表面的重力加速度 ;
;
(2)若测得该星球的半径为 m,宇航员要在该星球上发射一颗探测器绕其做匀速圆周运动,则探测器运行的最大速度为多大?
m,宇航员要在该星球上发射一颗探测器绕其做匀速圆周运动,则探测器运行的最大速度为多大?
如图所示,竖直放置的圆弧轨道和水平轨道两部分相连. 水平轨道的右侧有一质量为 2 m的滑块C 与轻质弹簧的一端相连,弹簧的另一端固定在竖直的墙M上,弹簧处于原长时,滑块C静止在P 点处;在水平轨道上方O 处,用长为L 的细线悬挂一质量为 m 的小球 B,B 球恰好与水平轨道相切,并可绕O点在竖直平面内摆动。质量为 m 的滑块A 由圆弧轨道上静止释放,进入水平轨道与小球B发生碰撞,A、B 碰撞前后速度发生交换. P 点左方的轨道光滑、右方粗糙,滑块A、C 与PM 段的动摩擦因数均为
B,B 球恰好与水平轨道相切,并可绕O点在竖直平面内摆动。质量为 m 的滑块A 由圆弧轨道上静止释放,进入水平轨道与小球B发生碰撞,A、B 碰撞前后速度发生交换. P 点左方的轨道光滑、右方粗糙,滑块A、C 与PM 段的动摩擦因数均为 =0.5,A、B、C 均可视为质点
=0.5,A、B、C 均可视为质点 ,重力加速度为g.
,重力加速度为g.
(1)求滑块A 从2L高度处由静止开始下滑, 与B碰后瞬间B的速度.
(2)若滑块A 能以与球B 碰前瞬间相同的速度与滑块C 相碰,A 至少要从距水平轨道多高的地方开始释放?
(3)在(2)中算出的最小值高度处由静止释放A,经一段时间A 与C 相碰,设碰撞时间极短, 碰后一起压缩弹簧,弹簧最大压缩量为
碰后一起压缩弹簧,弹簧最大压缩量为 L,求弹簧的最大弹性势能。
L,求弹簧的最大弹性势能。