如下图，质
量
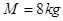的小车停放在光滑水平面上，在小车右端施加一水平恒力F=8N。当小车向右运动速度达到3m/s时，在小车的右端轻放一质量m
=2kg的小物块，物块与小车间
的动摩擦因数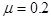
，假定小车足够长，试求：
（1）经过多长时间物块停止与小车间的相对运动？
（2）小
物块从放在车上开始经过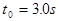
所通过的位移是多少？（g取
）
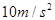如图所示,两个形状、大小相同的钢球A、B,A球质量为1.5kg, B球质量为0.5kg开始A球不带电,静止在高h=0.88m的光滑平台上,B球带0.3C的正电荷,用长L=1m的细线悬挂在平台上方,整个装置放在竖直向下的匀强电场中,场强大小E=10N/C.现将细线拉开角度α=600后,由静止释放B球,B球在最低点与A球发生对心碰撞,碰撞时无机械能损失,若碰后不考虑A、B球的相互作用,不计空气阻力,取g=10m/s2,求:
(1)B球刚摆到最低点时的速率;
(2)A球从离开平台到着地时的水平位移大小.
如图所示，在直角坐标系的第一、二象限内有垂直于纸面的匀强磁场，第三象限有沿y轴负方向的匀强电场；第四象限无电场和磁场。现有一质量为m、电荷量为q的粒子以速度v0从y轴上的M点沿x轴负方向进入电场，不计粒子的重力，粒子经x轴上的N点和P点最后又回到M点，设OM=L,ON=2L.求：
（1）带电粒子的电性，电场强度E的大小；
（2）带电粒子
到达N点时的速度大小和方向；
（3）匀强磁场的磁感应强B的大小和方向；
（4）粒子从M点进入电场，经N、P点最后又回到M点所用的时间。
如图所示，有一金属棒ab，质量m=40g，电阻R=2.8Ω，可以无摩擦地在两条轨道上滑动，轨道间的距离d=20cm，电阻不计，轨道平面与水平面间的夹角α=37
，置于竖直向上的匀强磁场中，回路中电池的电动势E=2v，内电阻r=0.2Ω，问磁感应强度B为多大时，金属棒恰好静止？(sin37=0.6，cos37=0.8，g取
10m/s
)
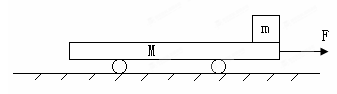
长L＝1.4m，高h＝1.25m，质量M＝30kg的木箱，在水平地面上滑行，木箱与地面间的动摩擦因数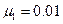
。当木箱的速度
1.2m/s时，把一质量为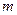
＝20kg的铁块轻轻地放在木箱顶的前端（铁块视为质点），铁块与木箱间动摩擦因数
，问
（1）铁块在木箱上怎样运动？
（2）铁块会从木箱的哪一端滑下来？铁块的落地点距木箱的滑落端的水平距离是多少？（g=10m/s2）
如图所示，一质量m=5kg物体静止在水平地面上，在斜向上的恒力F拉动下，开始向右运动。已知力F=50N，物体与地面间动摩擦因数µ=0.4，力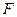
与水平方向的夹角
。（
，
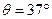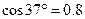，g=10m/s2）。
（1）求物体对地面的压力大小；
（2）求力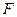作用5s时物体的速度大小；
（3）如果力F作用5s后撤去，则物体在从静止开始运动的15s内通过的位移是多大？