（本小题满分12分）某工厂生产一种产品的原材料费为每件40元，若用x表示该厂生产这种产品的总件数，则电力与机器保养等费用为每件0.05x元，又该厂职工工资固定支出12500元。
（1）把每件产品的成本费P（x）（元）表示成产品件数x的函数，并求每件产品的最低成本费；
（2）如果该厂生产的这种产品的数量x不超过3000件，且产品能全部销售，根据市场调查：每件产品的销售价Q（x）与产品件数x有如下关系：
，试问生产多少件产品，总利润最高？（总利润=总销售额-总的成本）
（本小题满分12分）已知函数
（1）若直线
过点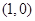
，并且与曲线
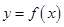相切，求直线的方程；
（2）设函数
在
上有且只有一个零点，求
的取值范围。（其中
为自然对数的底数）
（本小题满分12分）已知：过抛物线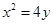
的焦点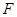
的直线交抛物线于
两个不同的点，过分别作抛物线的切线，且二者相交于点
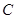
（1）求证：
；
（2）求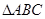
的面积的最小值。
（本小题满分12分）在三棱锥
中，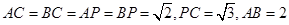
。
（1）求证：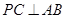
；
（2）求二面角
的余弦值的绝对值。
（本小题满分12分）为了解甲、乙两厂的产品质量，分别从两厂生产的产品中各随机抽取10件，测量产品中某种元素的含量（单位：毫克），其测量数据的茎叶图如下：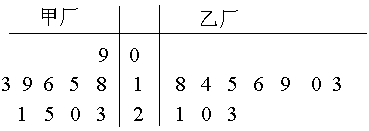
规定:当产品中此种元素含量大于18毫克时，认定该产品为优等品。
（1）试比较甲、乙两厂生产的产品中该种元素含量的平均值的大小；
（2）从乙厂抽出上述10件产品中，随机抽取3件，求抽到的3件产品中优等品数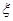
的分布列及数学期望。
（本小题满分12分）已知等差数列
的前
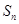项和为，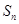
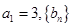为等比数列，且
，
。
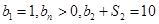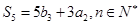（1）求数列，
的通项公式；
（2）求数列
的前n项和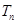
。