如图,椭圆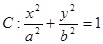
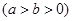 的顶点为
的顶点为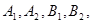 焦点为
焦点为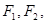
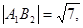 S□
S□ = 2S□
= 2S□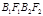 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线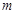 过
过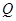 (1,1),且与椭圆相交于
(1,1),且与椭圆相交于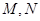 两点,当
两点,当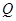 是
是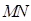 的中点时,求直线
的中点时,求直线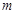 的方程.
的方程.
(Ⅲ)设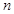 为过原点的直线,
为过原点的直线,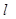 是与n垂直相交于P点且与椭圆相交于两点
是与n垂直相交于P点且与椭圆相交于两点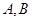 的直线,
的直线,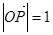 ,是否存在上述直线
,是否存在上述直线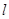 使以
使以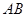 为直径的圆过原点?若存在,求出直线
为直径的圆过原点?若存在,求出直线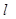 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.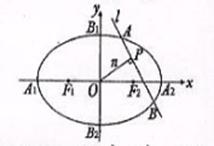
(本小题满分12分)如图,矩形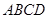 中,对角线
中,对角线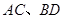 的交点为
的交点为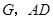 ⊥平面
⊥平面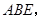
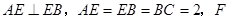 为
为 上的点,且
上的点,且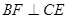 .
.
(I)求证: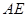 ⊥平面
⊥平面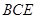 ;
;
(II)求三棱锥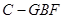 的体积.
的体积.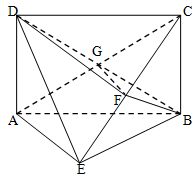
(本小题满分12分)某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.
(I)计算甲班7位学生成绩的方差 ;
;
(II)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.
参考公式:
方差 ,其中
,其中 .
.
(本小题满分12分)
已知 为等差数列,且满足
为等差数列,且满足 .
.
(I)求数列 的通项公式;
的通项公式;
(II)记 的前
的前 项和为
项和为 ,若
,若 成等比数列,求正整数
成等比数列,求正整数 的值.
的值.
设函数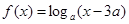
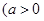 且
且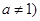 ,当点
,当点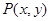 是函数
是函数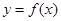 图象上的点时,点
图象上的点时,点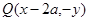 是函数
是函数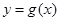 图象上的点.
图象上的点.
(1)写出函数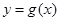 的解析式;
的解析式;
(2)若当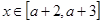 时,恒有
时,恒有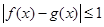 ,试确定
,试确定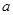 的取值范围.
的取值范围.
在直三棱柱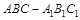 中,
中,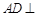 平面
平面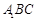 ,其垂足
,其垂足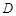 落在直线
落在直线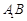 上.
上.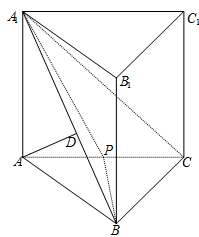
(Ⅰ)求证: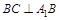 ;
;
(Ⅱ)若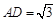 ,
,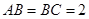 ,
,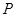 为
为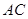 的中点,求三棱锥
的中点,求三棱锥 的体积.
的体积.