已知椭圆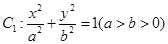 与直线
与直线 相交于
相交于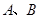 两点.
两点.
(1)若椭圆的半焦距 ,直线
,直线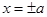 与
与 围成的矩形
围成的矩形 的面积为8,
的面积为8,
求椭圆的方程;
(2)若 (
(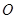 为坐标原点),求证:
为坐标原点),求证: ;
;
(3)在(2)的条件下,若椭圆的离心率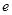 满足
满足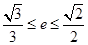 ,求椭圆长轴长的取值范围.
,求椭圆长轴长的取值范围.
数列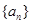 满足
满足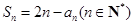 .
.
(1)计算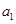 ,
, ,
, ,
,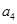 ,由此猜想通项公式
,由此猜想通项公式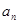 ,并用数学归纳法证明此猜想;
,并用数学归纳法证明此猜想;
(2)若数列 满足
满足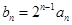 ,求证:
,求证: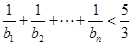 .
.
如图,在圆锥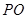 中,已知
中,已知 ,⊙O的直径
,⊙O的直径 ,
,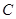 是
是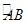 的中点,
的中点,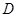 为
为 的中点.
的中点.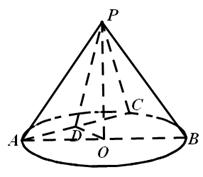
(1)证明:平面 平面
平面 ;
;
(2)求二面角 的余弦值.
的余弦值.
甲、乙两位篮球运动员进行定点投篮,甲投篮一次命中的概率为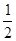 ,乙投篮一次命中的概率为
,乙投篮一次命中的概率为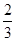 .每人各投4个球,两人投篮命中的概率互不影响.
.每人各投4个球,两人投篮命中的概率互不影响.
(1)求甲至多命中1个球且乙至少命中1个球的概率;
(2)若规定每投篮一次命中得3分,未命中得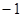 分,求乙所得分数
分,求乙所得分数 的概率分布和数学期望.
的概率分布和数学期望.
先后掷两颗均匀的骰子,问
(1)至少有一颗是6点的概率是多少?
(2)当第一颗骰子的点数为3或6时,求两颗骰子的点数之和大于8的概率.