如图,AB是⊙O的直径,点C是BA延长线上一点,CA=1,CD切⊙O于D点,弦DE∥CB,Q是AB上一动点,当DQ⊥AB时Q恰好为OA中点.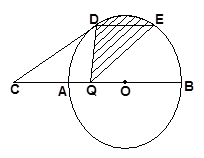
(1)求⊙O的半径R.
(2) 当点 Q从点A向点B运动的过程中,图中阴影部分的面积是否发生变化,若发生变化,请你说明理由;若不发生变化,请你求出阴影部分的面积.
为了保证2010年广州亚运会期间亚运会场馆和亚运村环境卫生的干净,亚运会管理委员会决定开展一次“清理垃圾”演练.演练垃圾重达150吨,由于演练方案准备充分,各方面协调有力,亚运会垃圾清运小组清理垃圾的速度比原来提高了一倍,结果提前3小时完成了任务,问垃圾清运小组原计划每小时清运多少吨的垃圾?
先化简,再求值: .其中m=5.
.其中m=5.
(1)已知x = -2,求 的值。
的值。
(2)解方程
某校师生积极为某地震灾区捐款,在得知灾区急需帐蓬后,立即到当地的一家帐蓬厂采购,帐蓬有两种规格:可供3人居住的小组帐蓬,价格为每顶160元;可供10人居住的大帐蓬,价格为每顶400元.学校共花去捐款96000元,正好可供2300人临时居住.
(1)求该校采购了多少顶3人小帐蓬?多少顶10人大帐蓬?
(2)学校计划租用甲、乙两种型号的卡车共20辆,把这批帐篷紧急运往灾区,已知甲型卡车每辆可同时装运4顶小帐篷和11顶大帐篷,乙型卡车每辆可同时装运12顶小帐篷 和7顶大帐篷,应如何安排甲、乙两种型号卡车可一次将这批帐篷运往灾区?有哪几种租车方案?
如图,在△ABC中,已知AD⊥BC,垂足为D,AE、BF分别是∠BAC、∠ABC的平分线,AE与BF相交于点O.
(1)当∠BAC=50°,∠C=70°时,求∠AED,∠AOB;
(2)当∠C= 时,求∠AOB.
时,求∠AOB.