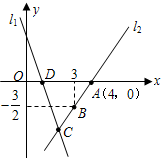
如图，直线l1的解析表达式为：
，且l1与x轴
交于点D，直线l2经过点A，B，直线l1，l2交于点C．（1）求直线l2的函数关系式；
（2）求△ADC的面积；
（3）若点H为坐标平面内任意一点，在坐标平面内是否存在这样的点H，使以A、D、C、H为顶点的四边形是平行四边形？若存在，请直接写出点H的坐标；若不存在，请说明理由．
某企业投资100万元引进一条农产品加工线，若不计维修、保养费用，预计投产后每年可获利33万元，该生产线投资后，从第1年到第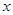
年的维修、保养费用累计为
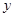（万元），且
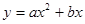，若第1年的维修、保养费用为2万元，第2年为4万元。
（1）求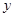与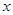之间的关系式；
（2）投产后，这个企业在第几年就能收回投资？
如图，在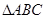
中，AD是BC边上的高，
。
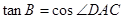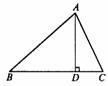
（1）求证：AC＝BD
（2）若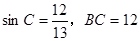
，求AD的长。
已知抛物线过点A（－1，0），B（0，6），对称轴为直线x＝1
（1）求抛物线的解析式
（2）画出抛物线的草图
（3）根据图象回答：当x取何值时，y>0
已知：关于x的方程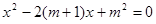
（1） 当m取何值时，方程有两个实数根？
（2） 为m选取一个合适的整数，使方程有两个不相等的实数根，并求这两个根.
如图,在△ABC中,∠C=90°，AD是∠BAC的平分线，AC=6，CD=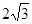
。
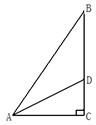
求（1）∠DAC的度数；（2）AB,BD的长。