经过天文望远镜的长期观测,人们在宇宙中已经发现了许多双星系统,通过对它们的研究,使我们对宇宙中的物质的存在形式和分布情况有了较深刻的认识。双星系统是由两个星体组成,其中每个星体的线度都远小于两个星体之间的距离。一般双星系统距离其他星体很远,可以当作孤立系统处理。现根据对某一双星系统的光学测量确定,该双星系统中每个星体的质量都是M,两者间距L,它们正围绕着两者连线的中点作圆周运动。试计算该双星系统的周期T;
若实验上观测到的运动周期为T’,为了解释两者的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的暗物质。作为一种简化模型,我们我们假定在以两个星体连线为直径的球体内均匀分布着密度为ρ的暗物质,而不考虑其它暗物质的影响,并假设暗物质与星体间的相互作用同样遵守万有引力定律。试根据这一模型计算双星系统的运动周期T’。
如图所示,x轴与水平传送带重合,坐标原点0在传送带的左端,传送带OQ长 L=8m,传送带顺时针速度V。=5m/s, —质量m=1kg的小物块轻轻放在传送带上xp="2m" 的P点,小物块随传送带运动到Q点后恰好能冲上光滑圆弧轨道的最高点N点。小物块与 传送带间的动摩擦因数μ.=0.5,重力加速度g= 10m/s2,求: 
(1)N点的纵坐标;
(2)若将小物块轻放在传送带上的某些位置,小物块均能沿光滑圆弧轨道运动(小物块始终 在圆弧轨道运动不脱轨)到达纵坐标yM=0.25m的M点,求这些位置的横坐标范围。
如图所示,滑块A套在光滑的坚直杆上,滑块A通过细绳绕过光滑滑轮连接物 块B,B又与一轻质弹贊连接在一起,轻质弹簧另一端固定在地面上,’开始用手托住物块 .使绳子刚好伸直处于水平位位置但无张力。现将A由静止释放.当A下滑到C点时(C点 图中未标出)A的速度刚好为零,此时B还没有到达滑轮位置,已知弹簧的劲度系数k="100N/m" ,滑轮质量和大小及摩擦可忽略不计,滑轮与杆的水平距离L=0.3m,AC距离为 0.4m,mB=lkg,重力加速度g="10" m/s2。试求: 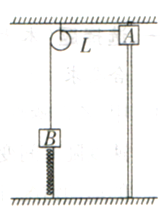
(1)滑'块A的质量mA
(2)若滑块A质量增加一倍,其他条件不变,仍让滑块A从静止滑到C点,则滑块A到达C点时A、B的速度大小分别是多少?
如图所示,一个截面为直角三角形的劈形物块固定在水平地面上.斜面,高h=4m,a=37°,一小球以Vo=9m/s的初速度由C点冲上斜面.由A点飞出落在AB面上.不计一切阻力.(Sin37°=0.6,cos37° =0.8,g="10" m/s2)求.
(l)小球到达A点的速度大小;
(2)小球由A点飞出至第一次落到AB面所用时间;
(3)小球第一次落到AB面时速度与AB面的夹角 的正切值
的正切值
质量,M=3kg的长木板放在光滑的水平面t在水平悄力F=11N作用下由静止开始 向右运动.如图所示,当速度达到1m/s2将质量m=4kg的物块轻轻放到本板的右端.已知物块与木板间摩擦因数μ=0.2,物块可视为质点.(g=10m/s2,).求: 
(1)物块刚放置木板上时,物块和木板加速度分别为多大?
(2)木板至少多长物块才能与木板最终保持相对静止?
(3)物块与木板相对静止后物块受到摩擦力大小?
如图所示,光滑水平面上有A、B、C三个物块,其质量分别为mA = 2.0kg,mB = 1.0kg,mC = 1.0kg.现用一轻弹簧将A、B两物块连接,并用力缓慢压缩弹簧使A、B两物块靠近,此过程外力做功W=108J(弹簧仍处于弹性限度内),然后同时释放A、B,弹簧开始逐渐变长,当弹簧刚好恢复原长时,C恰以4m/s的速度迎面与B发生碰撞并粘连在一起.求:
(1)弹簧刚好恢复原长时(B与C碰撞前)A和B物块速度的大小?
(2)当弹簧第二次被压缩时,弹簧具有的弹性势能为多少?