如图（甲）所示，M1M4、N1N4为平行放置的水平金属轨道，M4P、N4Q为相同半径，平行放置的竖直半圆形金属轨道，M4、N4为切点，P、Q为半圆轨道的最高点，轨道间距L=1.0m，圆轨道半径r=0.32m，整个装置左端接有阻值R=0.5Ω的定值电阻。M1M2N2N1、M3M4N4N3为等大的长方形区域Ⅰ、Ⅱ，两区域宽度 d=0.5m，两区域之间的距离s=1.0m；区域Ⅰ内分布着均匀的变化的磁场B1，变化规律如图（乙）所示，规定竖直向上为B1的正方向；区域Ⅱ内分布着匀强磁场B2，方向竖直向上。两磁场间的轨道与导体棒CD间的动摩擦因数为μ=0.2，M3N3右侧的直轨道及半圆形轨道均光滑。质量m=0.1kg，电阻R0=0.5Ω的导体棒CD在垂直于棒的水平恒力F拉动下，从M2N2处由静止开始运动，到达M3N3处撤去恒力F，CD棒匀速地穿过匀强磁场区，恰好通过半圆形轨道的最高点PQ处。若轨道电阻、空气阻力不计，运动过程导体棒与轨道接触良好且始终与轨道垂直，g取10m/s2求：
水平恒力F的大小；
CD棒在直轨道上运动过程中电阻R上产生的热量Q；
磁感应强度B2的大小。
某同学用一个测力计（弹簧秤）、木块和细线去粗略测定一木块跟一个固定斜面之间的动摩擦因数μ。设此斜面的倾角不大，不加拉力时，木块放在斜面上将保持静止。（1）他是否要用测力计称出木块所受的重力？（2）写出他实验的主要步骤。（3）推出求μ的计算式。
如图所示，竖直光滑杆上套一个小球和两根弹簧，两弹簧的一端各与小球相连，另一端分别用销钉M、N固定于杆上，小球处于静止状态。设拔去销钉M瞬间，小球加速度的大小为12m/s2。若不拔去销钉M而拔去销钉N瞬间，小球的加速度可能是（取g=10m/s2）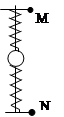
| A．22m/s2，竖直向上 | B．22m/s2，竖直向下 | C．2m/s2，竖直向上 | D．2m/s2，竖直向下 |
(18分)如图所示，在光滑绝缘的水平面内，对角线AC将边长为L的正方形分成ABC和ADC两个区域，ABC区域有垂直于水平面的匀强磁场，ADC区域有平行于DC并由C指向D的匀强电场。质量为m、带电量为+q的粒子从A点沿AB方向以
的速度射入磁场区域，从对角线AC的中点进入电场区域。
（1）判断磁场的方向并求出磁感强度B的大小。
（2）讨论电场强度E在不同取值时，带电粒子在电场中运动的时间t。
如图所示，质量为m的小球悬挂在长为L的细线下端，将它拉至与竖直方向成θ=60°的位置后自由释放．当小球摆至最低点时，恰好与水平面上原来静止的、质量为2m的木块相碰，碰后小球速度反向且动能是碰前动能的
．已知木块与地面的动摩擦因素μ=
，重力加速度取g．求：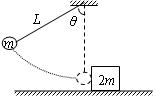
（1）小球与木块碰前瞬间所受拉力大小
（2）木块在水平地面上滑行的距离
两根足够长的光滑金属导轨平行固定在倾角为θ的斜面上，它们的间距为d．磁感应强度为B的匀强磁场充满整个空间、方向垂直于斜面向上．两根金属杆ab、cd的质量分别为m和2m，垂直于导轨水平放置在导轨上，如图所示．设杆和导轨形成的回路总电阻为R而且保持不变，重力加速度为g．
（1）给ab杆一个方向沿斜面向上的初速度，同时对ab杆施加一平行于导轨方向的恒定拉力，结果cd杆恰好保持静止而ab杆则保持匀速运动．求拉力做功的功率．
（2）若作用在ab杆的拉力与第（1）问相同，但两根杆都是同时从静止开始运动，求两根杆达到稳定状态时的速度．