q是第三象限角,方程x2+y2sinq=cosq表示的曲线是
| A.焦点在x轴上的椭圆 | B.焦点在y轴上的椭圆 |
| C.焦点在x轴上的双曲线 | D.焦点在y轴上的双曲线 |
将两个顶点在抛物线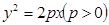 上,另一个顶点是此抛物线焦点的正三角形的个数记为
上,另一个顶点是此抛物线焦点的正三角形的个数记为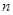 ,则()
,则()
A.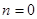 |
B.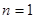 |
C.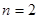 |
D.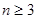 |
函数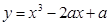 在
在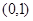 内有极小值,则实数
内有极小值,则实数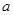 的取值范围为()
的取值范围为()
| A.(0,3) | B.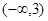 |
C.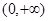 |
D.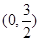 |
若执行如图1所示的框图,输入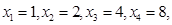 则输出的数等于()
则输出的数等于()
| A.15 | B.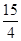 |
C.16 | D.4 |
某同学准备用反证法证明如下问题:函数f(x)在[0,1]上有意义,且f(0)=f(1),如果对于不同的x1,x2∈[0,1]都有|f(x1)-f(x2)|<|x1-x2|,求证:|f(x1)-f(x2)|<,那么它的假设应该是().
| A.“对于不同的x1,x2∈[0,1],都得|f(x1)-f(x2)|<|x1-x2| 则|f(x1)-f(x2)|≥” |
| B.“对于不同的x1,x2∈[0,1],都得|f(x1)-f(x2)|> |x1-x2| 则|f(x1)-f(x2)|≥” |
| C.“∃x1,x2∈[0,1],使得当|f(x1)-f(x2)|<|x1-x2| 时有|f(x1)-f(x2)|≥” |
| D.“∃x1,x2∈[0,1],使得当|f(x1)-f(x2)|>|x1-x2|时有|f(x1)-f(x2)|≥” |
 是虚数单位,计算
是虚数单位,计算 ()
()
| A.-1 | B.1 | C. |
D. |