(1)已知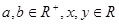 ,求证:
,求证: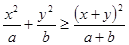 ;
;
(2)已知实数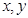 满足:
满足: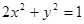 ,试利用(1)求
,试利用(1)求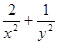 的最小值。
的最小值。
(本小题满分12分)如图,直三棱柱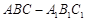 中,
中, ,
,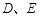 分别为
分别为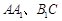 的中点,
的中点,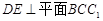 ,二面角
,二面角 的大小为
的大小为 .
.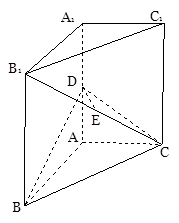
(Ⅰ)证明: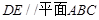 ;
;
(Ⅱ)求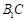 与平面
与平面 所成的角的大小.
所成的角的大小.
(本小题满分12分)甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为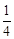 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为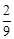 .
.
(Ⅰ)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(Ⅱ)若让每台机床各自加工2个零件(共计6个零件),求恰好有3个零件是一等品的概率.
(本小题满分12分)如图,在三棱锥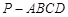 中 ,
中 ,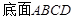 为正方形,
为正方形, ,
,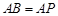 ,
,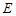 为
为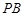 的中点.
的中点.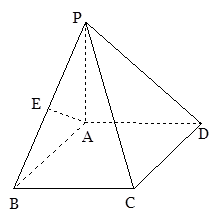
(Ⅰ)证明: ;
;
(Ⅱ)求二面角 的大小.
的大小.
(本小题满分12分)一个盒子中装有大小相同的2个红球和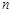 个白球,从中任取2个球.
个白球,从中任取2个球.
(Ⅰ)若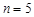 ,求取到的2个球恰好是一个红球和一个白球的概率;
,求取到的2个球恰好是一个红球和一个白球的概率;
(Ⅱ)若取到的2个球中至少有1个红球的概率为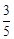 ,求
,求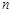 .
.
(本小题满分12分)已知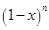 的展开式中第4项与第8项的二项式系数相等.
的展开式中第4项与第8项的二项式系数相等.
(Ⅰ)求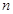 的值;
的值;
(Ⅱ)求第4项与第8项的系数之和.