在地面上有竖直放置的静止物体A和B,A、B之间用不计质量的轻弹簧栓接在一起,弹簧的劲度系数k=l00N/m,A、B的质量均为lkg,现用F=20N的竖直向上恒力作用在物体A上,使A竖直上升,重力加速度g=l0m/s2,设弹簧始终是在弹性限度内,空气阻力不计。
求:从力F开始作用到物体B刚离开地面的过程中拉力F做的功;
物体B刚离开地面时物体A的速度大小;
设物体B刚离开地面时弹簧的总长度为L,当B离开地面以后,弹簧第一次出现总长度等于L时,物体A、B的速度各为多大。
天空有近似等高的浓云层。为了测量云层的高度,在水平地面上与观测者的距离为d=3.0km处进行一次爆炸,观测者听到由空气直接传来的爆炸声和由云层反射来的爆炸声时间上相差Δt=6.0s。试估算云层下表面的高度。已知空气中的声速v=km/s。
原地起跳时,先屈腿下蹲,然后突然蹬地。从开始蹬地到离地是加速过程(视为匀加速),加速过程中重心上升的距离称为“加速距离”。离地后重心继续上升,在此过程中重心上升的最大距离称为“竖直高度”。现有下列数据:人原地上跳的“加速距离”d1=0.50m,“竖直高度”h1=1.0m;跳蚤原地上跳的“加速距离”d2=0.00080m,“竖直高度”h2=0.10m。假想人具有与跳蚤相等的起跳加速度,而“加速距离”仍为0.50m,则人上跳的“竖直高度”是多少?
质量m=1.5kg的物块(可视为质点)在水平恒力F作用下,从水平面上A点由静止开始运动,运动一段距离撤去该力,物块继续滑行t=2.0s停在B点,已知A、B两点间的距离s=5.0m,物块与水平面间的动摩擦因数μ=0.20,求恒力F多大。(g=10m/s2)
质量为10 kg的物体在F=200N的水平推力作用下,从粗糙斜面的底端由静止开始沿斜面运动,斜面固定不动,与水平地面的夹角θ=37°.力F作用2秒钟后撤去,物体在斜面上继续上滑了1.25秒钟后,速度减为零.求:物体与斜面间的动摩擦因数μ和物体的总位移S。(已知sin37°=0.6,cos37°=0.8,g=10 m/s2)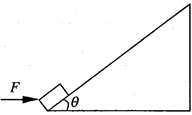
(1)下列核反应方程,正确的是.(填选项前的编号)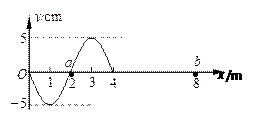
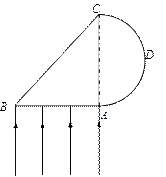
A.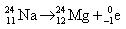 是聚变 是聚变 |
B.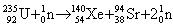 是裂变 是裂变 |
C. ,符号“X”表示中子 ,符号“X”表示中子 |
D.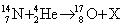 ,符号“X”表示中子 ,符号“X”表示中子 |
(2)质量为 M 的木块在光滑水平面上以速率v1向右运动,质量为m 的子弹以速率v2 水平向左射入木块,假设子弹射入木块后均未穿出,且在第N 颗子弹射入后,木块恰好停下来,求N 的数值.