正△ABC的边长为4,CD是AB边上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A—DC—B。
(I)试判断直线AB与平面DEF的位置关系,并说明理由;
(II)求二面角E—DF—C的余弦值;
(III)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论。
已知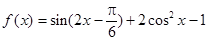
(Ⅰ)求函数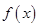 的单调增区间
的单调增区间
(Ⅱ)在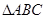 中,
中,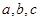 分别是角
分别是角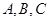 的对边,且
的对边,且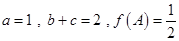 ,求
,求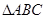 的面积
的面积
某糖果厂生产A、B两种糖果,A种糖果每箱可获利润40元,B种糖果每箱可获利润50元.其生产过程分混合、烹调、包装三道工序.下表为每箱糖果生产过程中所需平均时间(单位:min).
| 混合 |
烹调 |
包装 |
|
| A |
1 |
5 |
3 |
| B |
2 |
4 |
1 |
每种糖果的生产过程中,混合的设备至多用机器12 h,烹调的设备最多只能用机器30 h,包装的设备最多只能用机器15 h,每种糖果各生产多少箱可获得最大利润?
已知数列 是等差数列,且
是等差数列,且
(1)求数列 的通项公式;
的通项公式;
(2)(文)令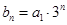 ,求
,求 的前n项和.
的前n项和.
(2)(理)令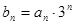 ,求
,求 的前n项和.
的前n项和.
在 中,
中,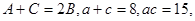 求
求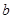 的值。
的值。
已知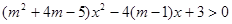 对一切实数
对一切实数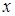 恒成立,求实数
恒成立,求实数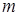 的范围
的范围