(选修4—4:坐标系与参数方程
以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线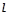 经过点P(1,1),倾斜角
经过点P(1,1),倾斜角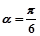 .
.
(1)写出直线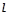 的参数方程;
的参数方程;
(2)设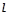 与圆
与圆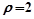 相交于两点A、B,求点P到A、B两点的距离之积.
相交于两点A、B,求点P到A、B两点的距离之积.
已知函数 ,求
,求 的值域和最小正周期。
的值域和最小正周期。
已知函数 ,(x>0),常数
,(x>0),常数 >0.
>0.
(Ⅰ)试确定函数 的单调区间;
的单调区间;
(Ⅱ)若对于任意 ,
, >0恒成立,试确定实数
>0恒成立,试确定实数 的取值范围;
的取值范围;
(Ⅲ)设函数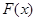 =
= +
+ ,求证:
,求证: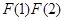 …
…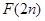 >
>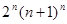 (
(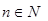 ,
,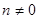 )
)
已知椭圆C: 的一条准线L方程为:x=
的一条准线L方程为:x=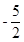 ,且左焦点F到L的距离为
,且左焦点F到L的距离为 .(Ⅰ)求椭圆C的方程;(Ⅱ)过点F的直线交椭圆C于两点A、B,交L于点M,若
.(Ⅰ)求椭圆C的方程;(Ⅱ)过点F的直线交椭圆C于两点A、B,交L于点M,若 ,
, ,证明
,证明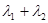 为定值.
为定值.
已知数列 中,
中, ,
,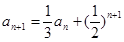 ,(Ⅰ)记
,(Ⅰ)记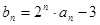 ,证明数列
,证明数列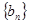 是等比数列;(Ⅱ)求数列
是等比数列;(Ⅱ)求数列 的通项公式.
的通项公式.
在某校举办的元旦有奖知识问答中,甲、乙、丙三人同时回答一道有关环保知识的问题,已知甲回答对这道题的概率是 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是 .(Ⅰ)求乙、丙两人各自回答对这道题的概率;(Ⅱ)用
.(Ⅰ)求乙、丙两人各自回答对这道题的概率;(Ⅱ)用 表示回答对该题的人数,求
表示回答对该题的人数,求 的分布列和数学期望E
的分布列和数学期望E .
.