(本题满分14分) 设等差数列{an}的首项a1为a,公差d=2,前n项和为Sn.
(Ⅰ) 若S1,S2,S4成等比数列,求数列{an}的通项公式;
(Ⅱ) 证明: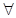 n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
已知抛物线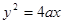 (
(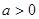 且
且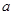 为常数),
为常数),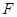 为其焦点.
为其焦点.
(1)写出焦点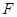 的坐标;
的坐标;
(2)过点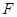 的直线与抛物线相交于
的直线与抛物线相交于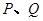 两点,且
两点,且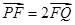 ,求直线
,求直线 的斜率;
的斜率;
(3)若线段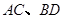 是过抛物线焦点
是过抛物线焦点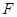 的两条动弦,且满足
的两条动弦,且满足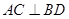 ,如图所示.求四边形
,如图所示.求四边形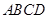 面积的最小值
面积的最小值 .
.
已知函数f(x)=2x-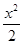 -aln(x+1),a∈R.
-aln(x+1),a∈R.
(1)若a=-4,求函数f(x)的单调区间;
(2)求y=f(x)的极值点(即函数取到极值时点的横坐标).
如图,双曲线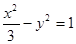 与抛物线
与抛物线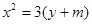 相交于
相交于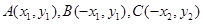
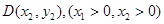 ,直线AC、BD的交点为P(0,p)。
,直线AC、BD的交点为P(0,p)。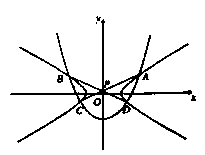
(I)试用m表示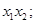
(II)当m变化时,求p的取值范围。
已知(x,y)在映射f下的象是(x+y,x2-y),其中x≥0,
求:(2,-2)的原象.
(1)已知函数y=ln(-x2+x-a)的定义域为(-2,3),求实数a的取值范围;
(2)已知函数y=ln(-x2+x-a)在(-2,3)上有意义,求实数a的取值范围.