设函数
(1)若关于x的不等式 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;
(2)设 ,若关于x的方程
,若关于x的方程 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.
(3)证明不等式:
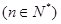
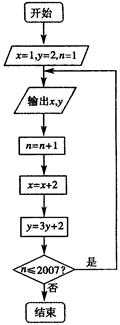
根据如图所示的程序框图,将输出的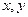 值依
值依
次分别记为 ;
;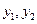 ,…,
,…,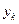 ,….
,….
(Ⅰ)分别求数列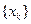 和
和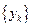 的通项公式;
的通项公式;
(Ⅱ)令 ,求数列
,求数列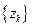 的前
的前 项和
项和 ,
, 其中
其中 .
.

一个空间几何体 的三视图如图所示,其中
的三视图如图所示,其中 分别是
分别是 五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形
五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形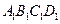 为正方形且
为正方形且 ;在左视图中
;在左视图中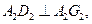 俯视图中
俯视图中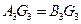 ,
,
(Ⅰ)根据三视图作出空间几何体 的直观图,并标明
的直观图,并标明 五点的位置;
五点的位置;
(Ⅱ)在空间几何体 中,过点
中,过点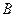 作平面
作平面 的垂线,若垂足H在直线
的垂线,若垂足H在直线 上,求证:平面
上,求证:平面 ⊥平面
⊥平面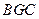 ;
;
(Ⅲ)在(Ⅱ)的条件下,求三棱锥 的体积及其外接球的表面积.
的体积及其外接球的表面积.
已知函数
(Ⅰ)若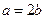 ,试问函数
,试问函数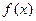 能否在
能否在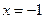 取到极值?若有可能,求出实数
取到极值?若有可能,求出实数 的值;否则说明理由.
的值;否则说明理由.
(Ⅱ)若函数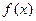 在区间(-1,2),(2,3)内各有一个极值点,试求
在区间(-1,2),(2,3)内各有一个极值点,试求 的取值范围.
的取值范围.
把一颗骰子投掷两次,第一次出现的点数记为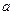 ,第二次出现的点数记为
,第二次出现的点数记为 ,试就方程组
,试就方程组 解答下列各题:
解答下列各题:
(Ⅰ)求方程组只有一组解的概率;
(Ⅱ)求方程组只有正数解的概率.
在△ABC中,三内角A、B、C及其对边a、b、c,满足sin(A-B)=sinB+sinC.
(Ⅰ)求角A的大小;
(Ⅱ)若a=6,求△ABC面积的最大值.