△ABC的三个顶点A(-3,0),B(2,1),C(-2,3).求:
(Ⅰ)BC边上中线AD所在直线的方程;
(Ⅱ)BC边上高线AH所在直线的方程.
(本小题满 10分)
10分)
设函数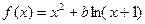 ,其中
,其中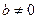 .
.
(1)若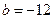 ,求
,求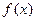 在
在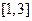 的最小值;
的最小值;
(2)如果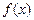 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数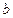 的取值范围;
的取值范围;
(本小题满分10分)
已知椭圆C的焦点F1(-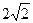 ,0)和F2(
,0)和F2(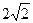 ,0),长轴长6,设直线
,0),长轴长6,设直线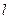 交椭圆C于A
交椭圆C于A B两点,且线段AB的中点坐标是P(-
B两点,且线段AB的中点坐标是P(-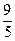 ,
,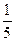 ),求直线
),求直线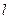 的方程。
的方程。
(本小题14分)
已知直线
 与椭圆
与椭圆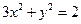 相交于
相交于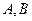 两点,
两点,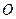 为坐标原点,
为坐标原点,
(1)求证: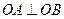 ;
;
(2)如果直线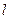 向下平移1个单位得到直线
向下平移1个单位得到直线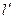 ,试求椭圆截直线
,试求椭圆截直线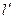 所得线段的长度。
所得线段的长度。
(本小题满分13分)
用长为18m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问:该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
本小题满分13分)
已知函数 =
=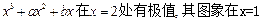 处的
处的 切线平行于直线
切线平行于直线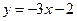 ,试求函数
,试求函数 的极值。
的极值。