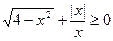(已知抛物线 ,过定点
,过定点 的直线
的直线 交抛物线于A、B两点.
交抛物线于A、B两点.
(Ⅰ)分别过A、B作抛物线的两条切线,A、B为切点,求证:这两条切线的交点 在定直线
在定直线 上.
上.
(Ⅱ)当 时,在抛物线上存在不同的两点P、Q关于直线
时,在抛物线上存在不同的两点P、Q关于直线 对称,弦长|PQ|中是否存在最大值?若存在,求其最大值(用
对称,弦长|PQ|中是否存在最大值?若存在,求其最大值(用 表示),若不存在,请说明理由.
表示),若不存在,请说明理由.
(本小题满分12分)某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站.记P到三个村庄的距离之和为y.
(1)设 ,求y
,求y 关于
关于 的函数关系式;
的函数关系式;
(2)变电站建于何处时,它到三个小 区的距离之和最小?
区的距离之和最小?
(本小题满分12分)在△ABC中,设角A,B,C的对边分别为a,b,c,若 ,
,
(1)求角A,B,C的大小;
(2)若BC边上的中线AM的长为 ,求△ABC的面积.
,求△ABC的面积.
(本小题满分12分)已知A,B,C三点的坐标分别为 ,
, ,
, ,其中
,其中 .
.
(1)若 ,求角
,求角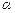 的值;
的值;
(2)若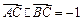 ,求
,求 的值.
的值.
设x, y, z ÎR, A + B + C =p,求证:
解下列关于x的不等式
(1) (2)
(2)