.(8分192班必做,其他班不做)
.已知函数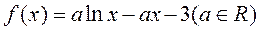 .
.
(1)当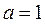 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)当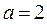 时,设函数
时,设函数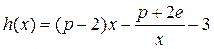 ,若在区间
,若在区间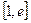 上至少存在一个
上至少存在一个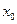 ,使得
,使得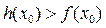 成立,求实数p的取值范围.
成立,求实数p的取值范围.
已知函数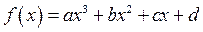 在
在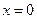 处取得极值,且过原点,曲线
处取得极值,且过原点,曲线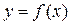 在P(-1,2)处的切线
在P(-1,2)处的切线 的斜率是-3
的斜率是-3
(1)求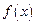 的解析式;
的解析式;
(2)若 在区间
在区间 上是增函数,数
上是增函数,数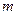 的取值范围;
的取值范围;
(3)若对任意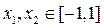 ,不等式
,不等式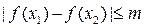 恒成立,求
恒成立,求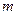 的最小值.
的最小值.
已知函数 是定义在
是定义在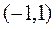 上的奇函数,且
上的奇函数,且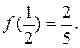
(1)确定函数 的解析式;
的解析式;
(2)判断并证明 在
在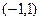 的单调性;
的单调性;
(3)解不等式
设命题 :函数
:函数 =x3-ax-1在区间
=x3-ax-1在区间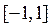 上单调递减;命题
上单调递减;命题 :函数
:函数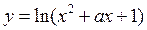 的值域是
的值域是 .如果命题
.如果命题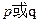 为真命题,
为真命题,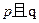 为假命题,求
为假命题,求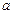 的取值范围.
的取值范围.
已知函数 =ax2+(b-8)x-a-ab , 当x
=ax2+(b-8)x-a-ab , 当x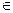 (-∞,-3)
(-∞,-3)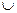 (2,+∞)时,
(2,+∞)时,  <0,当x
<0,当x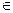 (-3,2)时
(-3,2)时 >0 .
>0 .
(1)求 在[0,1]内的值域.
在[0,1]内的值域.
(2)若ax2+bx+c≤0的解集为R,求实数c的取值范围.