如果a(1-a)4+a2(1+2a)k+a3(1+3a)2的展开式中含a4项的系数为114,求正整数k的值。
集合A与B各有12个元素,集合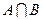 有4个元素,集合C满足条件:
有4个元素,集合C满足条件:
(1)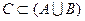 (2)C中含有3个元素; (3)
(2)C中含有3个元素; (3)
这样的集合C共有多少个?
4位学生与2位教师并坐合影留念.(1)教师必须坐在中间;(2)教师不能坐在两端,但要坐在一起;(3)教师不能坐在两端,且不能相邻.各有多少种不同的坐法?
(1)7人站成一排,要求较高的3个学生站在一起;
(2)7人站成一排,要求最高的站在中间,并向左、右两边看,身高逐个递减。
(3)任取6名学生,排成二排三列,使每一列的前排学生比后排学生矮。
一些棋手进行单循环制的围棋比赛,即每个棋手均要与其它棋手各赛一场,现有两名棋手各比赛3场后退出了比赛,且这两名棋手之间未进行比赛,最后比赛共进行了72场,问一开始共有多少人参加比赛?