探究函数 ,x∈(0,+∞)的最小值,并确定相应的x的值,列表如下:
,x∈(0,+∞)的最小值,并确定相应的x的值,列表如下:
| x |
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
| y |
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.102 |
4.24 |
4.3 |
5 |
5.8 |
7.57 |
… |
请观察表中y值随x值变化的特点,完成下列问题:
(1)若函数 ,(x>0)在区间(0,2)上递减,则在 上递增;
,(x>0)在区间(0,2)上递减,则在 上递增;
(2)当x= 时, ,(x>0)的最小值为 ;
,(x>0)的最小值为 ;
(3)试用定义证明 ,(x>0)在区间(0,2)上递减;
,(x>0)在区间(0,2)上递减;
(4)函数 ,(x<0)有最值吗?是最大值还是最小值?此时x为何值?
,(x<0)有最值吗?是最大值还是最小值?此时x为何值?
(5)解不等式 .
.
解题说明:(1)(2)两题的结果直接填写在横线上;(4)题直接回答,不需证明。
已知圆 的方程:
的方程: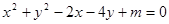
(1)求m的取值范围;
(2)若圆C与直线 相交于
相交于 ,
,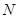 两点,且
两点,且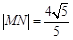 ,求
,求 的值
的值
(3)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m的值;
如图,在三棱柱 中,侧棱
中,侧棱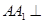 底面
底面 ,
, 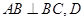 为
为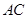 的中点,
的中点,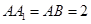 .
.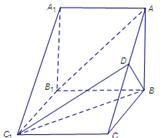
(1)求证: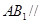 平面
平面 ;
;
(2)若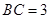 ,求三棱锥
,求三棱锥 的体积.
的体积.
某化肥厂有甲、乙两个车间包装肥料,在自动包装传送带上每隔30分钟抽取一包产品,称其重量(单位:kg),分别记录抽查数据如下:
甲:102,101,99,98,103,98,99;
乙:110,115,90,85,75,115,110.
(1)这种抽样方法是哪一种方法?
(2)试计算甲、乙车间产品重量的平均数与方差,并说明哪个车间产品较稳定?
箱子里有3双不同的手套,随机拿出2只,记事件A表示“拿出的手套配不成对”;事件B表示“拿出的都是同一只手上的手套”.
(1)请列出所有的基本事件;
(2)分别求事件A、事件B的概率.
已知圆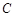 :
: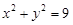 ,点
,点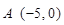 ,直线
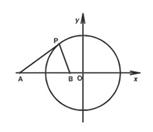
,直线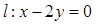 .
.
(1)求与圆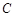 相切,且与直线
相切,且与直线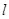 垂直的直线方程;
垂直的直线方程;
(2)在直线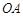 上(
上(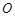 为坐标原点),存在定点
为坐标原点),存在定点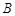 (不同于点
(不同于点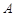 ),满足:对于圆
),满足:对于圆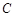 上的任一点
上的任一点 ,都有
,都有 为一常数,试求出所有满足条件的点
为一常数,试求出所有满足条件的点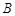 的坐标.
的坐标.