已知圆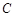
：
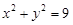，点
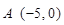，直线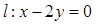
.
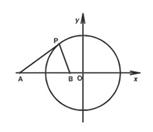
(1)求与圆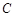相切，且与直线
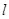垂直的直线方程；
（2）在直线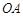
上（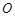
为坐标原点），存在定点
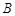（不同于点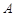
），满足：对于圆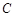上的任一点
，都有
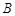为一常数，试求出所有满足条件的点的坐标.
（本小题满分12分）某公司为了实现2011年1000万元利润的目标，准备制定一个激励销售人员的奖励方案：销售利润达到10万元时，按销售利润进行奖励，且奖金数额y（单位：万元）随销售利润x（单位：万元）的增加而增加，但奖金数额不超过5万元，同时奖金数额不超过利润昀25%，现有三个奖励模型：
，问其中是否有模型能完全符合公司的要求？说明理由．
（参考数据：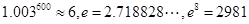
）
已知函数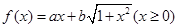
的图像经过（o，1），且
（1）求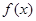
的值域；
（2）设命题
，命题q：函数
在R上无极值，是否存在实数m满足复合命题p且q为真命题？若存在，求出m的范围；若不存在，说明理由．
本小题满分12分）设函数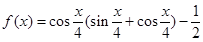
（1）求函数
取最值时x的取值集合；
（2）在△ABC中，角A、B、C的对边分别是a，b，c，且满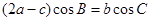
求函数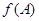
的取值范围．
(本小题满分14分)已知半径为
的圆的圆心在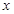
轴上，圆心的横坐标是整数，且与直线
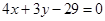相切．
（Ⅰ）求圆的方程；
（Ⅱ）设直线
与圆相交于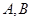
两点，求实数
的取值范围；
（Ⅲ） 在（Ⅱ）的条件下，是否存在实数，使得弦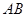
的垂直平分线
过点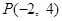
，若存在，求出实数的值；若不存在，请说明理由．
(本小题满分12分)如图，在底面是直角梯形的四棱锥S-ABCD中，
(1)求四棱锥S-ABCD的体积;
(2)求证：BC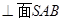
;
(3)求SC与底面ABCD所成角的正切值。