(本小题8分)如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为(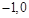 ),点B的坐标为(
),点B的坐标为(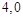 ),点C在y轴的正半轴上,且AB=OC.
),点C在y轴的正半轴上,且AB=OC.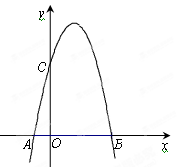
(1)求点C的坐标;
(2)求这个二次函数的解析式,并求出该函数的最大值.
如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长交边AD于点F,交CD的延长线于点G.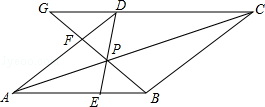
(1)求证:△APB≌△APD;
(2)已知DF:FA=1:2,设线段DP的长为x,线段PF的长为y.
①求y与x的函数关系式;
②当x=6时,求线段FG的长.
减负提质“1+5”行动计划是我市教育改革的一项重要举措.某中学“阅读与演讲社团”为了了解本校学生的每周课外阅读时间,采用随机抽样的方式进行了问卷调查,调查结果分为“2小时以内”、“2小时~3小时”、“3小时~4小时”和“4小时以上”四个等级,分别用A、B、C、D表示,根据调查结果绘制了如图所示的统计图,由图中所给出的信息解答下列问题:
(1)求出x的值,并将不完整的条形统计图补充完整;
(2)在此次调查活动中,初三(1)班的两个学习小组内各有2人每周课外阅读时间都是4小时以上,现从中任选2人去参加学校的知识抢答赛.用列表或画树状图的方法求选出的2人来自不同小组的概率.
先化简,再求值.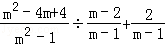 ,其中m=3.
,其中m=3.
如图,在平面直角坐标系中,抛物线y=﹣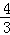 x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.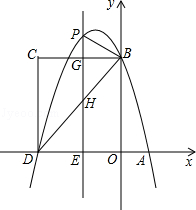
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
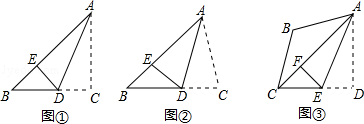
(1)操作发现:
如图①,在Rt△ABC中,∠C=2∠B=90°,点D是BC上一点,沿AD折叠△ADC,使得点C恰好落在AB上的点E处.请写出AB、AC、CD之间的关系 ;
(2)问题解决:
如图②,若(1)中∠C≠90°,其他条件不变,请猜想AB、AC、CD之间的关系,并证明你的结论;
(3)类比探究:
如图③,在四边形ABCD中,∠B=120°,∠D=90°,AB=BC,AD=DC,连接AC,点E是CD上一点,沿AE折叠,使得点D正好落在AC上的F处,若BC=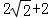 ,直接写出DE的长.
,直接写出DE的长.