（本小题满分6分）
如图，某人在点A处测量树高，点A到树的距离AD为21米，将一长为2米的标杆BE在与点A相距3米的点B处垂直立于地面，此时，观察视线恰好经过标杆顶点E及树的顶点C，求此树CD的高．
如图，一次函数y=2x﹣2的图象与x轴、y轴分别相交于B、A两点，与反比例函数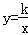
的图象在第一象限内的交点为M（3，m）．
（1）求反比例函数的解析式；
（2）在x轴上是否存在点P，使AM⊥PM？若存在，求出点P的坐标；若不存在，说明理由．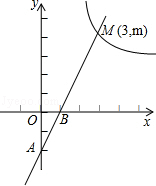
某公司从2009年开始投入技术改造资金，经技术改进后，其产品的生产成本不断降低，具体数据如表：
| 年度 |
2009 |
2010 |
2011 |
2012 |
| 投入技改资金x（万元） |
2.5 |
3 |
4 |
4.5 |
| 产品成本y（万元/件） |
7.2 |
6 |
4.5 |
4 |
（1）试判断：从上表中的数据看出，y与x符合你学过的哪个函数模型？请说明理由，并写出它的解析式．
（2）按照上述函数模型，若2013年已投入技改资金5万元
①预计生产成本每件比2012年降低多少元？
②如果打算在2013年把每件产品的成本降低到3.2万元，则还需投入技改资金多少万元？
如图所示，将长方形ABCD沿直线BD折叠，使C点落在C′处，BC′交AD于E．
（1）求证：BE=DE；
（2）若AD=8，AB=4，求△BED的面积．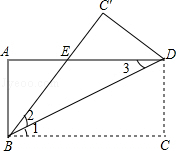
已知：y=y1+y2，y1与x2成正比例，y2与x成反比例，且x=1时，y=3；x=﹣1时，y=1．求x=﹣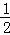
时，y的值．
问题探索
（1）计算与观察：把
的分子分母同时加上1，得到
，把
的分子分母同时加上2，得到
．比较
的大小关系： 
， （填“＞”、“＜”）
（2）归纳猜想：若正分数
（a＞b＞0）中的分子和分母同时加上正数m，得到
，结论又如何呢？ （填“＞”、“＜”）
（3）请证明你的猜想：