(本小题满分12分)
如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN ∥OB交CD于N.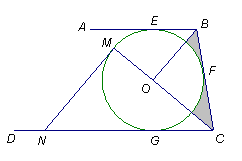
⑴求证:MN是⊙O的切线;
⑵当0B=6cm,OC=8cm时,求⊙O的半径及图中阴影部分的面积.
(1)通分: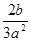 ,
, ;(2)通分:
;(2)通分: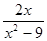 ,
,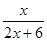 .
.
(1)约分: ;(2)约分:
;(2)约分: .
.
已知:△ABC中,AE平分∠BAC。
(1)如图①AD⊥BC于D,若∠C =70°,∠B =30°,则∠DAE=;
(2)如图②所示,在△ABC中AD⊥BC,AE平分∠BAC,F是AE上的任意一点,过F作FG⊥BC于G,且∠B=40°,∠C=80°,求∠EFG的度数;
(3)在(2)的条件下,若F点在AE的延长线上(如图③),其他条件不变,则∠EFG的角度大小发生改变吗?说明理由.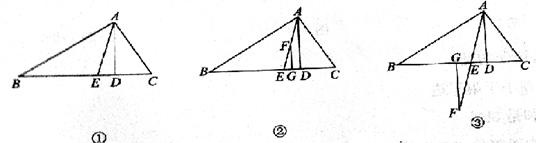
如图,梯形ABCD是由三个直角三角形拼成的,各直角边的长度如图所示。
(1)请你运用两种方法计算梯形ABCD的面积;
(2)根据(1)的计算,探索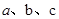 三者之间的关系,并用式子表示出来。
三者之间的关系,并用式子表示出来。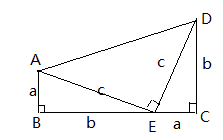
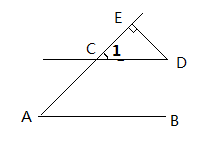
如图,AB∥CD,AE交CD与点C,DE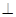 AE,垂足为E,
AE,垂足为E,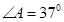 , 求
, 求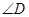 的度数。
的度数。