(本小题满分16分)设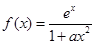 ,其中
,其中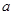 为正实数.
为正实数.
(1)当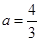 时,求
时,求 的极值点;
的极值点;
(2)若 为
为 上的单调函数,求
上的单调函数,求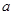 的取值范围.
的取值范围.
在平面直角坐标系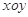 中,点
中,点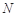 与点
与点 关于原点
关于原点 对称,
对称, 是动点,且直线
是动点,且直线 与
与
的斜率之积等于 .
.
(Ⅰ)求动点 的轨迹方程;
的轨迹方程;
(Ⅱ)设直线 和
和 与直线
与直线 分别交于
分别交于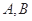 两点,问:是否存在点
两点,问:是否存在点 使得
使得 与
与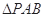 的面
的面
积相等?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知函数 (
(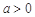 且
且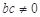 ).
).
(Ⅰ)若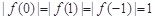 ,试求
,试求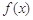 的解析式;
的解析式;
(Ⅱ)令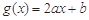 ,若
,若 ,又
,又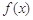 的图像在
的图像在 轴上截得的弦的长度为
轴上截得的弦的长度为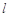 ,且
,且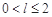 ,试比较
,试比较 、
、 的大小.
的大小.
已知关于x的一元二次方程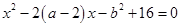 .
.
(1)若a、b是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
(2)若a∈[2,4],b∈[0,6],求方程没有实根的概率.
在锐角 中,内角
中,内角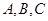 所对的边分别为
所对的边分别为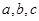 .已知
.已知 .
.
(Ⅰ)求角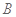 的大小;
的大小;
(Ⅱ)若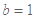 ,求
,求 的面积的最大值.
的面积的最大值.
已知命题 若非
若非 是
是 的充分不必要条件,求
的充分不必要条件,求 的取值范围.
的取值范围.