选修4—1:几何证明选讲
如图, 是圆的内接四边形,
是圆的内接四边形,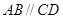 ,过
,过 点的圆的切线与
点的圆的切线与 的延长线交于
的延长线交于 点,证明:
点,证明:
(Ⅰ) ;
;
(Ⅱ) .
.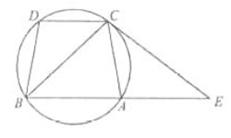
已知函数 ,
,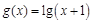 .
.
(Ⅰ)当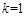 时,求函数
时,求函数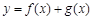 的单调区间;
的单调区间;
(Ⅱ)若方程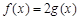 仅有一个实根,求实数
仅有一个实根,求实数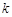 的取值集合.
的取值集合.
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当 时,车流速度
时,车流速度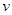 是车流密度x的一次函数.
是车流密度x的一次函数.
(Ⅰ)当 时,求函数
时,求函数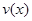 的表达式;
的表达式;
(Ⅱ)当车流密度 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时)。
可以达到最大,并求出最大值(精确到1辆/小时)。
已知 ,
, ,
,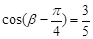 ,
, .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的值.
的值.
已知函数 .求:
.求:
(Ⅰ)函数 的对称轴方程;
的对称轴方程;
(Ⅱ)函数 在区间
在区间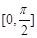 上的最值。
上的最值。
已知二次函数 满足
满足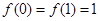 ,且
,且 ,求:
,求:
(Ⅰ) 的解析式;
的解析式;
(Ⅱ) 在
在 上的值域.
上的值域.