一袋子中有大小相同的2个红球和3个黑球，从袋子里随机取球，取到每个球的可能性是相同的，设取到一个红球得2分，取到一个黑球得1分。
（Ⅰ）若从袋子里一次随机取出3个球，求得4分的概率；
（Ⅱ）若从袋子里每次摸出一个球，看清颜色后放回，连续摸3次，求得分
的概率分布列及数学期望。
已知a≥b>0，求证：2a3－b3≥2ab2－a2b.
已知四棱锥P－ABCD的正视图是一个底边长为4，腰长为3的等腰三角形，如图分别是四棱锥P－ABCD的侧视图和俯视图．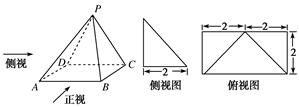
(1)求证：AD⊥PC；
(2)求四棱锥P－ABCD的侧面PAB的面积．
设角A，B，C为△ABC的三个内角．
(1)设f(A)＝sin A＋2sin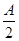 
，当A取A0时，f(A)取极大值f(A0)，试求A0和f(A0)的值；
(2)当A取A0时，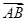
·
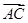＝－1，求BC边长的最小值．
如图，在几何体ABCDE中，AB＝AD＝2，AB⊥AD，AE⊥平面ABD，M为线段BD的中点，MC∥AE，且AE＝MC＝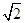
.
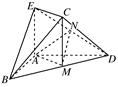
(1)求证：平面BCD⊥平面CDE；
(2)若N为线段DE的中点，求证：平面AMN∥平面BEC.
已知m＝(2cos x＋2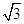
sin x,1)，n＝(cos x，－y)，且m⊥n.
(1)将y表示为x的函数f(x)，并求f(x)的单调递增区间；
(2)已知a，b，c分别为△ABC的三个内角A，B，C对应的边长，若f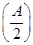
＝3，且a＝2，b＋c＝4，求△ABC的面积．