(本小题满分12分)泉城济南为增强市民的节水意识,面向全市征召宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组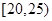 ,第2组
,第2组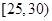 ,第3组
,第3组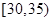 ,第4组
,第4组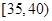 ,第5组
,第5组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(Ⅰ)若从第 组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从第
组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从第 组各抽取多少名志愿者?
组各抽取多少名志愿者?
(Ⅱ)在(Ⅰ)的条件下,决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
已知半径为2,圆心在直线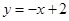 上的圆C.
上的圆C.
(Ⅰ)当圆C经过点A(2,2)且与 轴相切时,求圆C的方程;
轴相切时,求圆C的方程;
(Ⅱ)已知E(1,1),F(1,-3),若圆C上存在点Q,使 ,求圆心的横坐标
,求圆心的横坐标 的取值范围.
的取值范围.
如图,四边形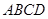 为菱形,
为菱形, 为平行四边形,且面
为平行四边形,且面
 面
面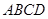 ,
,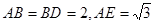 ,设
,设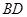 与
与 相交于点
相交于点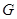 ,
, 为
为 的中点.
的中点.
(Ⅰ)证明: 面
面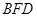 ;
;
(Ⅱ)若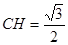 ,求
,求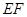 与面
与面 所成角的大小.
所成角的大小.
已知 的顶点
的顶点 ,
,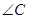 的平分线
的平分线 所在直线方程为
所在直线方程为 ,
, 边上的高
边上的高 所在直线方程为
所在直线方程为 .
.
(Ⅰ)求顶点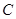 的坐标;
的坐标;
(Ⅱ)求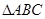 的面积.
的面积.
若某几何体的三视图(单位:cm)如图所示,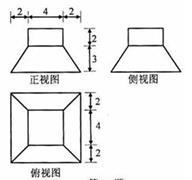
(Ⅰ)求此几何体的表面积;
(Ⅱ)求此几何体的体积.
已知圆 的圆心
的圆心 在
在 轴上,半径为2,直线
轴上,半径为2,直线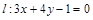 被圆
被圆 截得的弦长为
截得的弦长为 ,且圆心
,且圆心 在直线
在直线 的上方.
的上方.
(1)求圆 的方程;
的方程;
(2)设 ,
,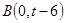 (2≤t≤4),若圆
(2≤t≤4),若圆 是
是 的内切圆,求
的内切圆,求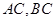 边所在直线的斜率(用
边所在直线的斜率(用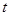 表示)
表示)
(3)在(2)的条件下求 的面积S的最大值及对应的
的面积S的最大值及对应的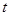 值.
值.