如图在直三棱柱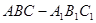
中,
.
(Ⅰ)求证: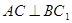
;(Ⅱ)求二面角
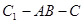的余弦值大小;
(Ⅲ)在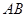
上是否存在点
,使得
∥平面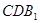
, 若存在,试给出证明;若不存在,请说明理由.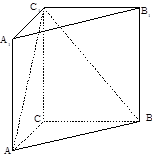
设命题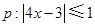
，命题
，若“
”为假命题，“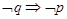
”为真命题，求实数
的取值范围
已知函数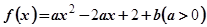
在区间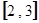
上的值域为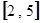
（1）求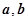
的值;
（2）若关于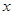
的函数
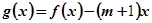在区间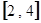
上为单调函数，求实数
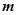的取值范围.
已知函数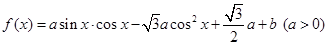
(1)求函数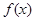
的最小正周期；
(2)设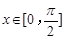
，
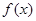的最小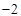值是
，最大值是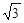
，求实数
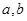的值．
已知a、b、c是△ABC的三条边，它们所对的角分别是A、B、C，若a、b、c成等比数列，且a2－c2＝ac－bc，试求
⑴角A的度数；
⑵求证：
；
（3）求
的值.
已知椭圆C：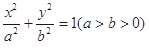
．
（1）若椭圆的长轴长为4，离心率为
，求椭圆的标准方程；
（2）在（1）的条件下，设过定点M（0，2）的直线l与椭圆C交于不同的两点A、B，且∠AOB为锐角（其中O为坐标原点），求直线l的斜率k的取值范围