设命题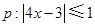 ,命题
,命题 ,若“
,若“ ”为假命题,“
”为假命题,“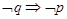 ”为真命题,求实数
”为真命题,求实数 的取值范围
的取值范围
已知函数 .
.
(1)求函数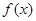 的极值;
的极值;
(2)若对任意的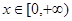 ,都有
,都有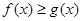 ,求实数a的取值范围.
,求实数a的取值范围.
某大学自主招生面试时将20名学生平均分成甲,乙两组,其中甲组有4名女学生,乙组有6名女学生.现采用分层抽样(层内采用不放回简单随即抽样)从甲、乙两组中共抽取4名学生进行第一轮面试.
(Ⅰ)求从甲、乙两组各抽取的人数;
(Ⅱ)求从甲组抽取的学生中恰有1名女学生的概率;
(Ⅲ)求抽取的4名学生中恰有2名男学生的概率.
设函数
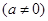 为奇函数,其图象在点
为奇函数,其图象在点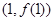 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数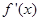 的最小值为
的最小值为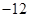 .
.
(Ⅰ)求 ,
, ,
,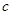 的值;
的值;
(Ⅱ)求函数 的单调递增区间,并求函数
的单调递增区间,并求函数 在
在 上的最大值和最小值.
上的最大值和最小值.
如图,在四棱椎P-ABCD中,底面ABCD是边长为 的正方形,且PD=
的正方形,且PD= ,PA=PC=
,PA=PC= .
.
(1)求证:直线PD⊥面ABCD;
(2)求二面角A-PB-D的大小.
某生物学习小组对 、
、 两种珍惜植物种子的发芽率进行实验性实验,每实验一次均种下一粒
两种珍惜植物种子的发芽率进行实验性实验,每实验一次均种下一粒 种子和一粒
种子和一粒 种子.已知
种子.已知 、
、 两种种子在一定条件下每粒发芽的概率分别为
两种种子在一定条件下每粒发芽的概率分别为 .假设任何两粒种子是否发芽相互之间没有影响.
.假设任何两粒种子是否发芽相互之间没有影响.
(Ⅰ)求3粒 种子,至少有1粒未发芽的概率;
种子,至少有1粒未发芽的概率;
(Ⅱ)求 、
、 各3粒种子,
各3粒种子, 至少2粒发芽且
至少2粒发芽且 全发芽的概率.
全发芽的概率.