如图,已知AB是⊙O的直径,CD是⊙O的切线,C为切点,连接AC,过点A作AD⊥CD于点D,交⊙O于点E.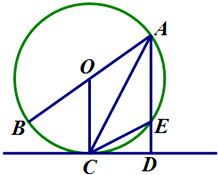
(Ⅰ)证明:∠AOC=2∠ACD;(Ⅱ)证明:AB•CD=AC•CE.
已知函数f(x)=ex﹣m﹣ln(2x).
(Ⅰ)设x=1是函数f(x)的极值点,求m的值并讨论f(x)的单调性;
(Ⅱ)当m≤2时,证明:f(x)>﹣ln2.
如图,已知椭圆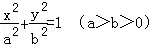 的右顶点为A(2,0),点P(2e,
的右顶点为A(2,0),点P(2e,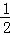 )在椭圆上(e为椭圆的离心率).
)在椭圆上(e为椭圆的离心率).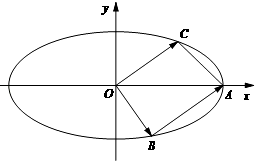
(1)求椭圆的方程;
(2)若点B,C(C在第一象限)都在椭圆上,满足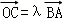 ,且
,且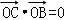 ,求实数λ的值.
,求实数λ的值.
甲、乙两人玩投篮游戏,规则如下:两人轮流投篮,每人至多投2次,甲先投,若有人投中即停止投篮,结束游戏,已知甲每次投中的概率为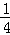 ,乙每次投中的概率为
,乙每次投中的概率为 求:
求:
(Ⅰ)乙投篮次数不超过1次的概率.
(Ⅱ)记甲、乙两人投篮次数和为ξ,求ξ的分布列和数学期望.
如图,DA⊥平面ABC,DA∥PC,∠ACB=90°,AC=AD=BC=1,PC=2,E为PB的中点.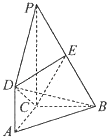
(Ⅰ)求证:DE∥平面ABC;
(Ⅱ)求二面角E﹣CD﹣B的余弦值.