请你设计一个包装盒,如图所示,ABCD是边长为60cm的 正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.
正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.
(1)若广告商要求包 装盒侧面积S(cm2)最大,试问x应取何值?
装盒侧面积S(cm2)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.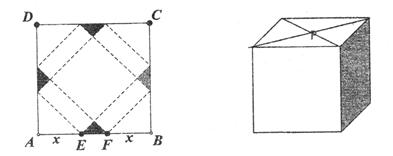
.一个袋中装有四个形状大小完全相同的球,球的编号分别为 .
.
(Ⅰ)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为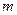 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为 ,求
,求 的概率.
的概率.
(本小题满分10分)
选修4-5:不等式选讲
已知对于任意非零实数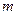 ,不等式
,不等式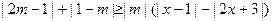 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
选做题(10分.请考生必须在22、23题中任选一题做答,如果多做,则按所做的第一题记分)
22.(本小题满分10分)
选修4-1:几何证明选讲
在 中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
(1)求证: ;
;
(2)若AC=3,求 的值。
的值。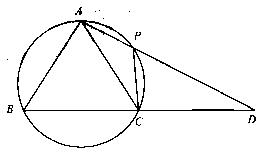
(12 分)
已知函数 .
.
①当 时,求
时,求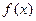 的最小值;
的最小值;
②若函数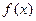 在区间
在区间 上为单调函数,求实数
上为单调函数,求实数 的取值范围;
的取值范围;
③当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知定点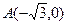 ,B是圆
,B是圆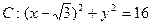 (C为圆心)上的动点,AB的垂直平分线与BC交于点E.
(C为圆心)上的动点,AB的垂直平分线与BC交于点E.
(1)求动点E的轨迹方程;
(2)设直线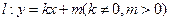 与E的轨迹交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:
与E的轨迹交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求: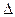 OPQ面积的最大值及此时直线
OPQ面积的最大值及此时直线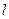 的方程.
的方程.