在平面直角坐标系中,角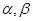 的始边为
的始边为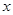 轴的非负半轴,点
轴的非负半轴,点 在角
在角 的终边上,点Q
的终边上,点Q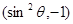 在角
在角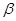 的终边上,且
的终边上,且 .
.
(1)求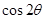 ;
;
(2)求P,Q的坐标,并求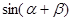 的值.
的值.
B.选修4—2 矩阵与变换
已知矩阵
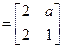 ,其中
,其中 ,若点
,若点 在矩阵
在矩阵 的变换下得到点
的变换下得到点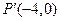 ,
,
(1)求实数a的值;
(2)求矩阵 的特征值及其对应的特征向量.
的特征值及其对应的特征向量.
A.选修4—1 几何证明选讲
在直径是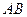 的半圆上有两点
的半圆上有两点 ,设
,设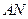 与
与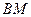 的交点是
的交点是 .
.
求证:

.
已知各项均不为零的数列{an}的前n项和为Sn,且满足a 1=c,2Sn=anan+1+r.
1=c,2Sn=anan+1+r.
(1)若r=-6,数列{an}能否成为等差数列?若能,求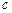 满足的条件;若不能,请说明理由.
满足的条件;若不能,请说明理由.
(2)设 ,
, ,
,
若r>c>4,求证:对于一切n∈N*,不等式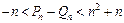 恒成立.
恒成立.
已知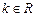 ,函数
,函数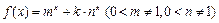 .
.
(1) 如果实数 满足
满足 ,函数
,函数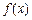 是否具有奇偶性?如果有,求出相应的
是否具有奇偶性?如果有,求出相应的
值,如果没有,说明为什么?
(2) 如果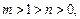 判断函数
判断函数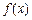 的单调性;
的单调性;
(3) 如果 ,
,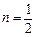 ,且
,且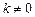 ,求函数
,求函数 的对称轴或对称中心.
的对称轴或对称中心.
如图,直角三角形ABC中,∠B= ,AB=1,B
,AB=1,B C=
C=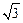 .点M,N分别在边AB和AC
.点M,N分别在边AB和AC
上(M点和B点不重合),将△AMN沿MN翻折,△AMN变为△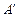 MN,使顶点
MN,使顶点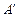 落
落
在边BC上(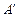 点和B点不重合).设∠AMN=
点和B点不重合).设∠AMN=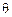 .
.
(1) 用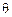 表示线段
表示线段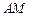 的长度,并写出
的长度,并写出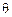 的取值范围;
的取值范围;
(2) 求线段 长度的最小值.
长度的最小值.